I was skimming through a book [1] the other day and saw the following three equations:
log 1.3712885742 = 0.13712885742
log 237.5812087593 = 2.375812087593
log 3550.2601815865 = 3.5502601815865
The sequence of digits is the same on both sides of each equation, except for the position of the decimal point.
The book said “The determination of such numbers has been discussed by Euler and by Professor Tait.” I don’t know who Professor Tait was, but I’ve heard of Euler. I’m curious why Euler was interested in this problem, whether it was idle curiosity inspired by looking up logarithms for some calculation or whether it was part of some larger exploration.
Evidently the logarithms above are taken base 10, and you could formulate the problem as finding solutions to
log10 x = 10k x
for integer k.
For a given k, how many solutions are there?
We could rephrase the question by looking for solutions to
log10(log10 x) − log10 x = k.
A plot shows that the left side is always negative and takes on every negative integer value twice, so there are no solutions for non-negative integers and two solutions for each negative integer.
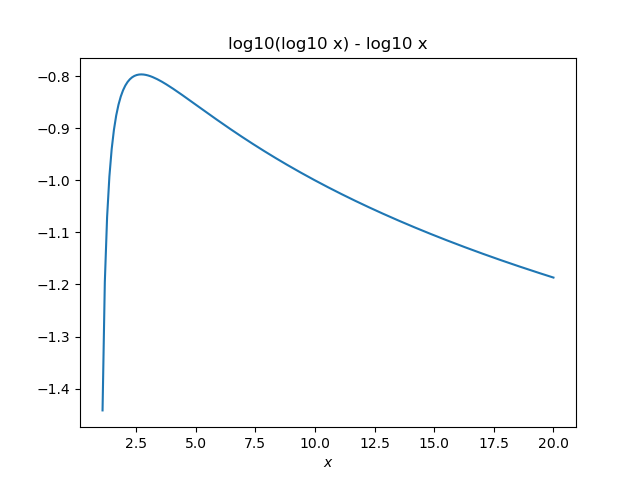
So, for example, when k = 3 there are two solutions. One is given at the top of the post. The other is x = 1.0023105706421267.
General bases
Would it make much difference if you were to generalize the problem to solving
logb x = bk x
for an arbitrary base b > 1?
Using the fact that
logb x = ln x / ln b
and a little algebra we can formulate the question as looking for solutions to
ln (ln x) − ln x = ln (ln b) + k ln b.
The function on the left hand side takes on the value 0 once and it takes on every negative value twice. The function on the right hand side is positive for positive k, which means no solutions exist in any base b > 1 when k = 0. There is one solution when b = e. Otherwise there are two solutions for negative integers k for each base b.
[1] A Scrap-Book of Elementary Mathematics: Notes, Recreations, Essays by William Frank White, 1908. Available on Project Gutenberg.
The post When log(x) has the same digits as x first appeared on John D. Cook.