While poking into the connection between Poisson equations, vector fields, and specialized neural networks, I decided to create custom vector field visualizations and I would like to present a few of the practical applications of calculus. If you own a boat, airplane, or car, by the end of this post you should be able to decide which path is best to take and when in order to save some precious money. Meaning we would rather have a tailwind for most of our journey than a strong headwind.

The goal of this post is to find the most aligned path through space. In order to achieve that I am going to use some mostly basic concepts like Work and Cost function. My goal is not to find an optimal path in the sense of Optimal control so by the end of this blog we are not going to know the exact consumption per flight or sail but we should be able to say: “Given a vector field, this path should give us minimal resistance.” However I might revisit the concept of Optimal control in the future, especially in combination with neural networks, these fields are very connected.

The solution presented in this post is a combination of WebGL2 and TypeScript. WebGL ideas are implemented from scratch, but some computational parts would be time-consuming to implement by myself, i.e. symbolic manipulation of equations or noise generation, however, usage of such code snippets should have zero impact on the possibility to understand the code itself by the reader.

Make Some Noise

In general, the weather forecast or current wind situation is described via wind barbs, which basically give you the direction and speed of the wind at a certain position (longitude, latitude, altitude). Data points like this form a vector field (associated scalar value and direction at each point in space) but there are also other types of fields like scalar field — i.e. temperature at each point in space. In my home project vector field data corresponds to some problems I am solving but for the case of fuel consumption and this post let’s use noise as a generator.

To generate the vector field, we are going to use Simplex noise. There is one important performance characteristic to Simplex noise, it scales very nicely with a dimension of the generated noise — in contrast with i.e. Perlin noise. Our vector field is going to be time-dependent, so we need to generate 4D noise and every frame is basically going to be a 3D slice in that 4D space. I do not have space to go into the details why Simplex noise has better performance because it would be another whole blog post but you can find a lot of resources on the web.

For our use case, I used Simplex implementation from this source. The reasoning behind this decision is the possibility to use the calculation directly in shaders and also because the code is pretty readable. Our Noise function’s N(x, y, z, t) output is a value between <0, 1.0). Internally we need three random values per vector:

• angle in XY plane
• angle in the XZ plane
• vector size

Each triplet is obtained by sampling of a Noise function with different constant offsets to z param. Offset is selected so there is no intersection of values, meaning XY angle is N(x, y, z, t), XZ angle is N(x, y, z + offset, t) and vector size is N(x, y, z + 2*offset, t). Important note, different noise implementations will have different function ranges, meaning you are not always going to get values between <0, 1.0).

Visualization of the vector field can be seen below. Apart from vectors, you can also see noise rendered to texture — either separated as grayscale or combined into RGB to three channels.

Space is split into n planes along the Z axis. Each plane is then rendered to an offscreen texture. In general, we would not need to render the entire noise field, but we do so anyway for visualization purposes. As you can see, the bottom layer shows what the noise field actually looks like; it is a time-dependent grayscale image. Once we have the offscreen textures, we can then draw our vectors (currently 400 vectors per plane). The angle and size of the vectors are obtained from the textures via a texel fetch in the shader. You can dynamically add more layers in the user interface.

Flow, Do You Feel It?

Vectors are pretty good as a visualization tool for current vector field state, but sometimes it is better to get flow field visualization so you also get some kind of interval time-based behavior of the whole system. And that is also our third visualization tool. Since WebGL is a kinda limited framework ( usage of compute or geometry shaders is wild west ), we are going to render the flow field into the texture. The simplified pipeline is:

1. Generate N random points in space at time T and save positions to buffers B1 and B2
2. Draw points in B1 to texture
3. Render texture and then lower the alpha value of the texture, which gives us tail of particles over time
4. Calculate position of points at time T+Epsilon based on current vector field (our Noise function) and save the result to B2, basically B2 = Noise({B1})
5. Switch buffers B1 and B2
6. Go to second step

However, for this stage, we will not use any offscreen textures, as we did when we wanted to render the noise. Since we are only interested in calculating over a dataset (particles represented as points), we will use WebGL’s Transform Feedback feature. This approach is a little bit better than using textures ping-pong for GPGPU. We can work directly with the data, meaning there is no room for sampling ambiguity. I am not saying that sampling of a texture or texel fetch is somehow broken, but I would not bet my life on the precision of the obtained data and that it will never be interpolated in some way. But maybe I am just overly suspicious, and any implementation works well. :] Red color represents faster particles.

As I mentioned, our Noise function is implemented in shaders, so usage of Noise is straightforward together with Transform feedback. I did not test the performance deeply but it should be pretty good from a scaling point of view since we touch our particles just twice, calculate new positions and draw calls. In this particular case flow visualization might not be that interesting but I am using that as a visualization of the projected surface gradient field to a 2D plane and it is more useful than navigating through the 3D space.

Where Is The Airplane, Lebowski?

So we have our vector field, we also have a set of few visualization techniques and the only thing we are missing is actually the airplane and path of our flight. In general, we want to be able to calculate the Cost of the travel no matter which path we have but to make our case at least somehow close to real life, we should pick some path similar to actual flight.

I decided to start with the Bump function. It is symmetrical, can have a long plateau relative to domain size and somehow represents aggressive take-off or landing.

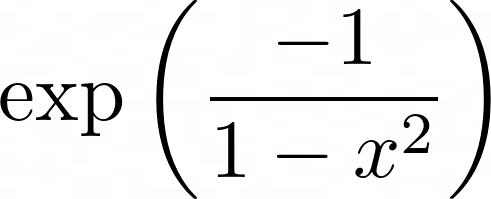
Visualization of paths in WebGL is, well, not ideal. We could spend a lot of time working on path representation in space but I have bigger fish to fry so I made a deal with the devil and we have to be satisfied with representation via LINE_STRIP. Given any function, program samples function at N points and make a strip through the vector field. As you can see, at any sample point, there is also a visualization of vector value at that point and time.

Cost Of Flight

We are going to dig into more complicated stuff later but as a start we are going to use the basic definition of Work done when a particle is traveling through the vector field along some path. So in our case let’s pretend that plane is just a particle. Regarding the intuition, this integral basically just says how well aligned our path is with the current time-dependent vector field. Meaning that getting a positive value, tailwind was stronger, and getting a negative value, the head wind was stronger.

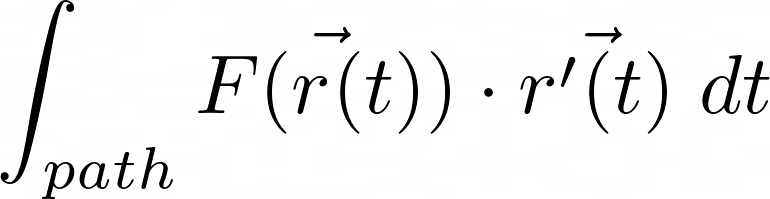
Where r is a parameterized function of our path through the vector field, F is our vector field defined by the Noise function, evaluated at the path and we want to integrate over time t. Also, before integration, we have to do a dot product with the derivation of our parameterized function. Now this is all fine and dandy, but only until the point you actually start to integrate the expression. We have multiple issues solving this analytically. But before we get into it, let’s look at our Noise function.

Akima? Hai

The definition of Simplex noise is basically written in our shader, so we might think that using it as an input to our integral is fine. After all, when we simplify the calculation of noise for the sake of argument, it is just a bunch of nice operations on polynomials that are easy to integrate.

The problem is that we need to apply sin and cos functions to get vector coefficients. And to integrate these functions, we are getting into the zone of generalized Fresnel integrals. These integrals can be solved and enumerated, but it is a lot of work. And the question is whether we want to handle complex analysis in a similar project without using a backend like Matlab or Scipy.

But there is another argument for solving this issue in a different manner. Often, you do not know the definition of a vector field because all of the data you have comes from thousands of sensors. And yes, you could somehow model the dynamic system or even train or overfit a neural network to get pretty good ODEs or PDEs, but that is not an easy task.

Instead, we will do the following. We will sample our Noise function at N points along the path r to get our random triplets (XY angle, XZ angle, vector size). Then, we will apply sin/cos projections to get the components of our vectors. As a final touch, we will apply Akima spline interpolation to those data points so we get three continuous piecewise cubic polynomial functions (in total, N-1 polynomials per each component).

Akima spline is an interesting type of spline because it is pretty quick to compute and especially useful when you do not have strong requirements, such as continuous derivatives of nth order. In our case, we only need the first derivative. It also behaves well, the average error is small, and sometimes many of those polynomials will be linear or constant.

This also means that our single integral will be split into N-1 integrals that we just need to summarize together. In theory, we could multiply each approximation with a step function or an analytical approximation of the heaviside function to make sure the spline is “active” only on its domain. However, this would complicate the final integral even more.

The Bump Function Is Not Civilized

So far so good, vector field is approximated by polynomials and now we need to somehow handle the second part of the dot product, derivation of parameterized path function r. Let’s look at our dot product:

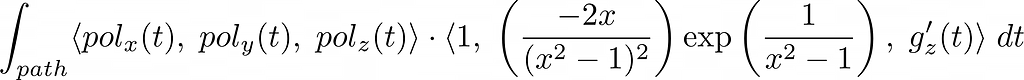
Where pol is Akima’s interpolation (polynomial) of vector field along the path and g(t) is the z component of our path parametrized in terms of t. Below you can see two examples of g(t) function, one is constant 0, and one is sin(t). We are now able to construct any meaningful path through the vector field:

Derivation of the bump function is not that bad, but we need to realize that it is going to be multiplied within the dot product with cubic polynomials and that is our next problem. Integrals like that could be solved only numerically and that is something we do not want to necessarily do.

And for that reason, we are going to interpolate the derivation of parameterized path function via Akima splines as well. Now, the dot product is going to produce a polynomial of order at most 6, and integration of polynomials is fine and dandy, finally without any sarcasm.

In case you are planning to play around with the live demo or even source code, you can add any number of paths in FlightHelper class. You can use any symbolic representation you want to but it has to be compatible with Nerdamer. For example, this is a definition for functions you saw in previous pictures:

static init() {
  this.flightPaths = new Array<FlightPath>()
  this.flightPaths.push(
    new FlightPath("sin(3x)", "e^(-1/(1-x^2))")
  )

  for( let i = 0; i < 5; i++) {
    let offset = "" + (1 + 0.1i) + "*"
    this.flightPaths.push(
      new FlightPath("0", offset + "e^(-1/(1-x^2))")
    )
  }
}

Let There Be Results

I have to admit that I have been a little bit nervous about numeric stability and if the calculated work is going to be precise enough — especially with multiple Akima interpolations. It ended up better than expected as you can see on the video below.

When the vector field is aligned with our path, the result of work is 2, which makes sense, since the domain size is exactly 2. When the vector field works against us, the result of work is -2 and when the vector field is perpendicular, work is 0. In the next video, you can see the calculation when the vector field is randomized by noise. Once done, the best path is colored black, and the cost for every path is shown in the left upper corner.

Technical note, calculation of approximations and final Nerdamer’s integration had to be moved to Worker so it is not blocking the main thread. And because Worker does not have high priority, the calculation takes between 1 and 2 seconds. In production settings it would make sense to run everything on server side anyways, especially because we could use scipy, Matlab or some other fast and fined tool for math operations.

But Plane Is Not Just A Point

So far we were able to calculate how aligned the vector field is with our path. Although our calculation is not a precise model, we can now tell which path is somehow better or worse from an energetic point of view. If we could select the time, when we are going to fly from Prague to Tokyo in our private jet, we could calculate the working coefficient based on weather prediction and probably save a lot of money for fuel since we selected the most aligned prediction. But we could do that with any other means of transportation. I.e. If you own a boat, instead of data on wind weather prediction, you could use wave velocity combined with wind prediction and the task is the same, just in fewer dimensions.

I have no ambition to have a precise model of fuel consumption, but there is one thing we could do right away and that could improve our calculation. Instead of just Work integral, let’s add another function to our integral, and lets call it Cost:

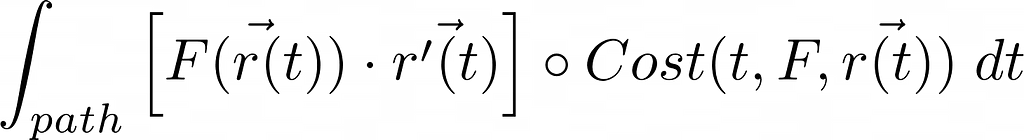
This function can represent a whole set of dynamic characteristics like:

• Headwind at 45 degrees might have a different impact than a tailwind at 45 degrees
• While in take-off phase, any headwind from the vector field should have a bigger weight on the final Work integral
• The longer we fly, the bigger impact wind has since we burn fuel
• Somehow we could even propagate the aerodynamic profile of the airplane, meaning different coefficients per angle
• So far we also neglected the airplane’s thrust, which is probably also a dynamic system regarding the influence of vector field

Cost function might be very complicated, and without a physical plane or detailed model, it is impossible to predict. However, we can experiment with different ideas, same as I am experimenting with this concept while solving something regarding the Poisson equations. Also, the application of Cost function might differ in different cases, it does not have to be just multiplication but Cost might be the operator as well.

Show Me The Path, My Lord

We are now in a position where we can choose when we are going to fly to our destination and let’s say we can also select our path — this in general is not true, air space is no anarchy. From a mathematical point of view, we are just looking for the global minimum of our Work integral and we can get candidates for such minimums while looking for derivatives that are equal to zero:

Solving this problem might not be easy, especially when Cost function is going to be complicated — take that just as a concept/idea, because in practice these problems are solved differently. But we have other options that might work kinda well, especially in the real world. So far these options are not yet implemented in the project since I did not need them, but I might add them in the future.

One solution would be to split the world into the 3D grid and find the best way in a graph i.e. via A*. Since the grid is going to be regular, we can apply spline interpolation to our paths as well. Additionally, we might have a set of rules like:

• Euclidean distance from the start of the path to the current position must always increase and at the same time euclidean distance from current position to end of the path must always decrease
• Any point on the grid must be inside some envelope

Another solution might be “monte carlo”-like. Generate n paths, calculate their Work, pick some best subset, and for each subset generate another set of similar paths. The number of iterations is up to you and how precise you need to be. Since the vector field is going to be continuous and any metrics on that field are going to be continuous as well, we should get pretty good candidates for our flight. The last sentence is very speculative but if we are talking about wind or any nature-related phenomena, it seems counterintuitive to me to have some region with a lot of expensive paths but with a special valley with a local minimum inside the same region.

So far I did not mention one thing. Time t used for path parameterization and for vector field sampling was addressed as uniformly distributed value on line. However, that was just a simplification. While in take off phase, t should move slower since we would travel smaller distance than while traveling in cruise phase. Or as a simpler example, t might represent mapping to path length. Again, it depends on our use case. So in general we would approach our time as:

Once we have some sort of non-linear distribution of time per path, our calculations should be pretty good. It might complicate our equations but as long as we use some kind of spline interpolation, we should be fine. In some cases, when vector field does not change that much, approximation by linear time might be pretty good as well. It depends on our use-case.

Future Plans

Initially, I wanted to make this post about Poisson equations but in the end visualization subtask took me longer than expected and I also added more features on the way. Nevertheless, I am glad it ended up this way since even a subtask like this contains a lot of interesting bits. A live demo is available on GitHub, as well as source code — everything related to this project is in the webgl2 folder. There are still a few parts I would like to optimize better (speed up noise calculation/path cost, better orbit camera, fewer draw calls (instanced arrays, remove duplicate uniforms), etc). For now, usage on a desktop/laptop is preferred.

In my next blog post, I would like to visit some ideas about neural networks and Poisson equations and I would also like to move from WebGL to WebGPU, this time developed as a desktop application, so I am going to use C++ or Rust, but Rust seems like more fun. Thank you for your time and feel free to comment. Also, my LaTeX skill is rusty, so I am really sorry for any harm I inflicted on LaTeX OGs.

Vector Fields and Fuel Consumption Wrapped in 3D was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.