The sinc function
sinc(x) = sin(x) / x
comes up continually in signal processing. If x is moderately small, the approximation
sinc(x) ≈ (2 + cos(x))/3
is remarkably good, with an error on the order of x4/180. This could be useful in situations where you’re working with the sinc function and the x in the denominator is awkward to deal with and you’d rather have a pure trig function.
Here’s a plot:
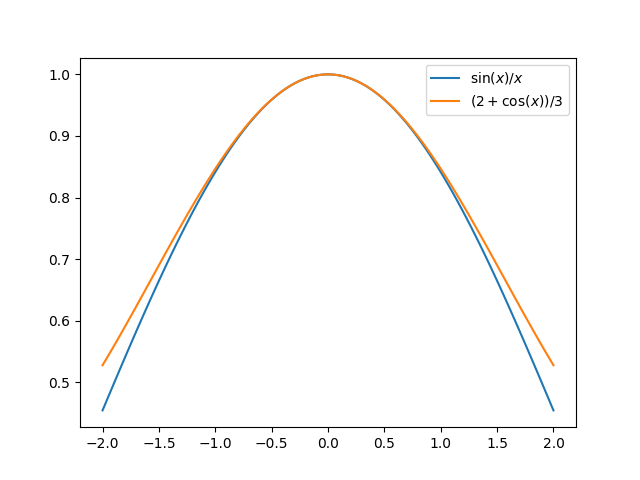
Of course the approximation is only good for small x. For large x the sinc function approaches zero while (2 + cos(x))/3 oscillates with constant amplitude forever.
When the approximation is good, it is very, very good, which reminds me of this nursery rhyme.
There was a little girl,
Who had a little curl,
Right in the middle of her forehead.
When she was good,
She was very, very good,
But when she was bad, she was horrid.
More sinc posts
The post Sinc function approximation first appeared on John D. Cook.