I was skimming through the book Mathematical Reflections [1] recently. He was discussing a set of generalizations [2] of the Star of David theorem from combinatorics.

gcdleft(binom{n - 1}{r - 1}, binom{n}{r+1}, binom{n+1}{r}right) = gcdleft(binom{n-1}{r}, binom{n+1}{r+1}, binom{n}{r-1}right)

The theorem is so named because if you draw a Star of David by connecting points in Pascal’s triangle then each side corresponds to the vertices of a triangle.

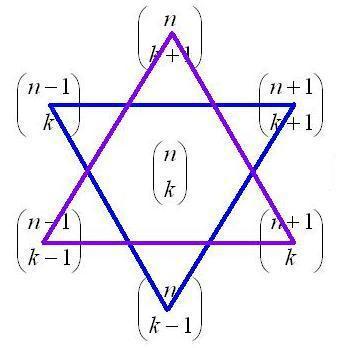
diagram illustrating the Star of David Theorem

One such theorem was the following.

binom{n - ell}{r - ell} binom{n - k}{r} binom{n - k - ell}{r - k} = binom{n-k}{r-k} binom{n - ell}{r} binom{n - k - ell}{r - ell}

This theorem also has a geometric interpretation, connecting vertices within Pascal’s triangle.

The authors point out that the binomial coefficient is a separable function of three variables, and that their generalized Star of David theorem is true for any separable function of three variables.

The binomial coefficient C(n, k) is a function of two variables, but you can think of it as a function of three variables: n, k, and n − k. That is

{n choose k} = f(n) , g(k) , g(n-k)

where f(n) = n! and g(k) = 1/k!.

I was surprised to see the term separable function outside of a PDE context. My graduate work was in partial differential equations, and so when I hear separable function my mind goes to separation of variables as a technique for solving PDEs.

Coincidentally, I was looking a separable coordinate systems recently. These are coordinate systems in which the Helmholtz equation can be solved by separable function, i.e. a coordinate system in which the separation of variables technique will work. The Laplacian can take on very different forms in different coordinate systems, and if possible you’d like to choose a coordinate system in which a PDE you care about is separable.

Related posts

[1] Peter Hilton, Derek Holton, and Jean Pedersen. Mathematical Reflections. Springer, 1996.

[2] Hilton et al refer to a set of theorems as generalizations of the Star of David theorem, but these theorems are not strictly generalizations in the sense that the original theorem is clearly a special case of the generalized theorems. The theorems are related, and I imagine with more effort I could see how to prove the older theorem from the newer ones, but it’s not immediately obvious.

The post Separable functions in different contexts first appeared on John D. Cook.

Previous Post
Next Post