Rigid Body Simulation Basics — Part 1: From Newton’s Law to a Constrained Optimization Problem

August 21, 2023
Rss Fetcher

Rigid Body Simulation Basics — Part 1: From Newton’s Law to a Constrained Optimization Problem

Screen captures from constraint-based rigid body simulators by author

Introduction

This article is intended to be the first article in a series where I plan to discuss some important topics on real-time physics simulation and build an engine incrementally. This first article attempts to explain the core idea of the velocity-space constraint-based physics simulation. It has a small sample program that works on Linux, OpenGL, and iOS with ARKit & Metal [Demo Video]. The core simulation part is written in plain C++.

With this article and the sample code, I hope the readers will be able to not only deduce the equations and recreate the algorithms by themselves but also to be able to understand the entire working code for a small simulation so that they can get a wholesome perspective view of the simulation technique and can apply the technique to their own games, interactive applications, and visual effects.

One thing not covered in this article: How to construct velocity-space constraints from the positional constraints?

That will be the topic for the second article.

Background

There are already many great books, such as physics-based animation by Erleben, Sporring, & Henriksen 2005 [ESHD05], and tutorials on the net, such as SIGGRAPH course nodes. They usually cover a wide range of topics regarding the physics engine, including affine transformations, geometric tests & operations, torques, orientation in quaternion, inertia tensor, collision detections, etc.

That’s a vast amount of information, and when the readers get to the parts where the constraint-based model is discussed, they may find it a bit challenging to grasp the core idea of the constraint-based model. Also, as the constraint-based model is presented in the context of full-fledged 3D simulation that involves both local and global coordinate systems, orientation, inertia tensor, etc., the equations presented in the text are cluttered and difficult to follow.

On the other hand, the lecture notes and course notes are usually compact and very well organized, but for first-time learners, it may be difficult to follow, as the math is usually in generalized compact forms, and there are lots of omissions that are obvious for the experienced practitioners and researchers. Either way, the LCP, and the Lagrangian multipliers are taken for granted, with little argument as to why they are introduced.

In my view, what’s missing is a compact introductory material with which interested readers can follow the flow of the argument without being stuck in the minutiae and can grasp the core idea of the velocity-space constraint-based physics simulation. That was the motivation for this article.

Organization

This article is organized as follows. We limit the argument to the two-dimensional linear motions and omit the treatment of the angular motions and orientations.

We derive the numerical integration step as the initial value problem of the ODE derived from Newton’s second law.
We introduce the linear constraints in the velocity space and the concept of the feasible region.
We find the best feasible solution by minimizing the total momentum applied to make corrections.
We model it as a constrained quadratic optimization problem.
We solve the problem for the Lagrangian multipliers with an MLCP solver.
We describe a basic framework for one simulation step, which can be transformed into a computer implementation.
We briefly look at the code in C++ in the sample program.

Intended Audience

Anybody interested in the real-time physics engine with a basic understanding of elementary classical mechanics, elementary Calculus, elementary Geometry, and elementary linear algebra.

Starting Point: Newton-Euler’s Second Law of Motion

The most important equations are given in Newton-Euler’s second law of motion as follows:

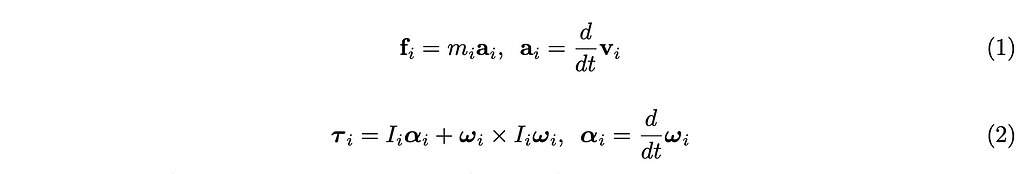
First equation: fi=miai, ai=(d/dt)vi Second equation: ti=Iiai+wixIiwi, ai=(d/dt) wi

where fᵢ is the force applied to the center of mass of the rigid body i, mᵢ is the mass, and aᵢ is the acceleration, vᵢ is the linear velocity. On the 2nd equation, τᵢ is the torque applied around the center of mass of the rigid body i, αᵢ is the angular acceleration, ωᵢ is the angular velocity, and Iᵢ ∈ R³ˣ³ is the inertia tensor, which changes dynamically depending on the orientation of the rigid body relative to the world coordinate system.

The relationship between the linear velocity vᵢ and the position xᵢ of the center-of-mass of the rigid body i is defined as follows.

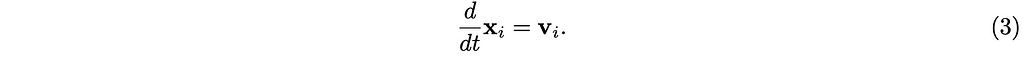
And the relationship between the angular velocity ωᵢ and the orientation qᵢ in quaternion can be defined as follows:

You don’t have to understand this article’s equations (2) and (4). The point is that we can treat the linear and angular motions independently. This article limits our discussion to the two-dimensional linear velocity and position. If we included the treatment of angles in quaternion, inertia tensor, torque, etc., then the equations would be very cluttered and harder to follow. In the future articles, we will expand the argument to include the two-dimensional rotation and orientation, and then three-dimensional orientation & rotation incrementally.

If you want to learn the angular motions by (2) and (4) now, I recommend you read Chap. 22, “Basic Classical Mechanics” of the book [ESHD05].
There are also plenty of good tutorials available on the internet for those topics.

What a Rigid-Body Physics Engine Does

A physics engine generates the positions and velocities of rigid bodies at discrete time steps (t₀, t₁, t₂, …), usually at the frame rate of 20–60 [fps] or sometimes higher. The behavior of the physics engine is mainly governed by Newton’s second law of motion as in the equation (2) and (5).
This is the most important equation:

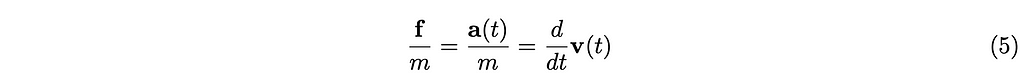
In this article, we handle something called velocity-space constraint-based physics simulation, meaning we integrate the equation above repeatedly to find vᵢ(t) at the given time steps.

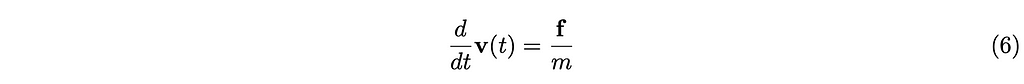
The position is then derived by integrating the following equation 7 after vᵢ(t) has been found.

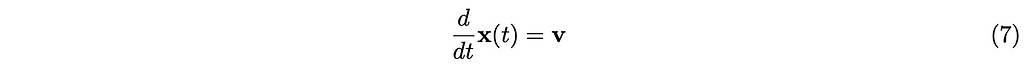
On the contrary, the positions are directly solved in the ‘position-based’ physics simulation. It’s been an active research area. In this article, we deal with the velocity-space simulation, as, in my view, it is still the main technique in the industry, and it is easier to understand.

The integration of equation (6) derives the following initial value problem, where t_c is the current time, and t_c+∆t is the next time step for which we want to find the velocities and positions.

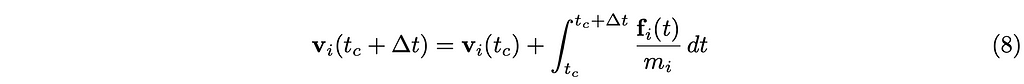
The problem is essentially to find vᵢ(t_c + ∆t) from vᵢ(t_c) and fᵢi(t), t_c ≤ t ≤ t_c + ∆t. There are several ways to solve this numerically, such as Runge-Kutta method. In particle physics simulation, the Verlet integration has been widely used. The Verlet integration requires the positions of the bodies at the previous time step t_c−∆t. If you are interested in the numerical integration of ODEs, you can read Chap. 8 of [AH05]. In this article, we use the simplest one, called the Euler method, as follows:

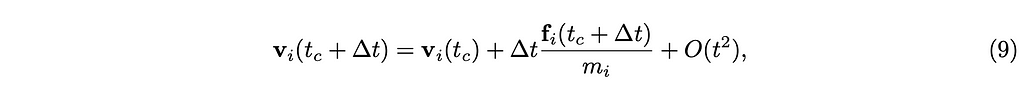
where O(t²) denotes the error term, and the position is derived in the same way as follows.

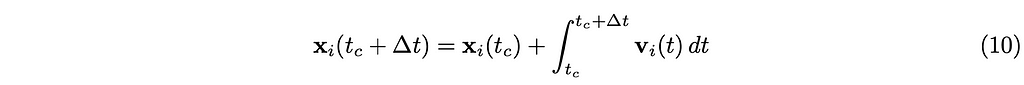
and with the Euler method,

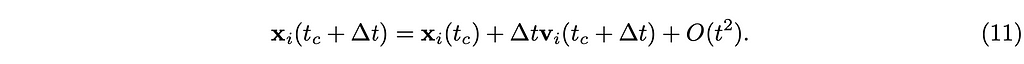
The error term of the Euler method is the highest of all the numerical integration methods. For example, the error term for Runge-Kutta is O(t⁴). This is usually not a problem for most of the use cases, as the errors will be corrected by the constraints, which will be described later.

However, if you want to simulate some trajectories accurately, for example, if you want to simulate the behavior of a javelin thrown by an athlete in a game, you would like to use a more accurate method than Euler.

This is the basis of the rigid body simulation. With only the numerical integration of Newton-Euler’s second law, we can merely express some orbital planetary motions, but nothing interesting that you want to see in the interactive applications can happen. One way to achieve more realistic and interesting behavior is to add constraints. Let’s look at the constraints in the next section.

Velocity space constraints

In the rigid body simulation, constraints keep a coffee cup resting on a table from falling through it. Constraints also keep the attachments of a joint together. As we are dealing with ‘velocity-space’ simulation, the constraints are expressed in terms of velocity.

Unilateral and bilateral constraints

The following is a unilateral (inequality) constraint i between rigid bodies k0 and k1.

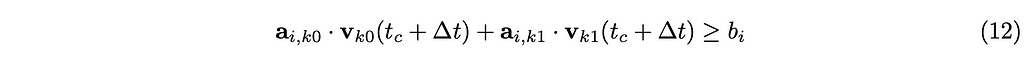
This defines the relationship between the velocities vₖ₀ and vₖ₁ of two rigid bodies, k0 and k1. The aᵢ,ₖ₀ and aᵢ,ₖ₁ are usually the unit vectors along which the impulse is applied. Intuitively, the scalar bᵢ can be considered a kind of ‘tightness’ of the constraint. The less the value is, the looser the constraint is, i.e., the more breathing space or margin the constraint has. The greater the value is, the tighter the constraint is, i.e., the more impulse will have to be applied to keep the rigid bodies under the constraint.

I will explain the impulses later. Such a crude interpretation of a and b can be useful later when you start working on the implementation.

And the following is called a bilateral (equality) constraint i between two objects k0 and k1.

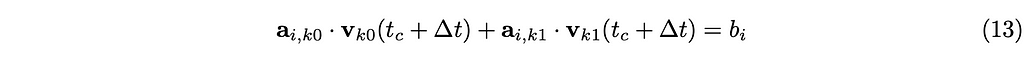
The bilateral constraints are mainly used for joints. The only difference from the unilateral constraints is the equality ‘=’. The intuitive interpretation of the scalar bᵢ is a bit different for the bilateral constraints. The negative values mean that the impulses in the opposite directions to aᵢ,ₖ₀ and aᵢ,ₖ₁ will more likely to be applied. The positive values mean that the impulses in the same directions to aᵢ,ₖ₀ and aᵢ,ₖ₁ will more likely to be applied. You will understand this later when we talk about the impulses.

If you want to define constraints between one rigid body k0 against the world, i.e., against a static fixture, rather than against another rigid body, then the constraints will have only one term as follows:

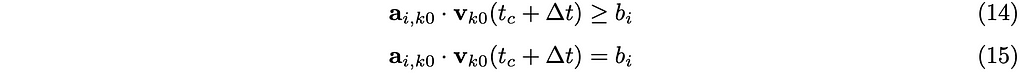
We could define constraints among three or more rigid bodies, but they would not be of any practical use. (Maybe it could be used if you want to confine three rigid bodies in a simplex or on the boundary of a simplex.)

At each time step t_c, you define a set of unilateral and bilateral constraints, which limits the region in which vₖ(t_c+∆t), 0≤ k≤K are allowed to reside, assuming there are K rigid bodies. If we concatenate all vₖ(t_c+∆t) into one big vector u(t_c+∆t), it will become a vector of dimension 2K, as we are dealing with two-dimensional linear velocity, and the set of unilateral and bilateral constraints defines the region in which it can reside. As the constraints are all in linear terms, the region is an open or closed polygon in the 2K-dimensional space. It is called a feasible region R.

If u(t_c+∆t) ∈ R, then u(t_c+∆t) is called a feasible solution.

Conventional matrix notation

Here I’d like to introduce a matrix J and a vector b to handle the constraints more succinctly and organized. They are the convention in the books and the literature. The matrix J aggregates all the coefficients a on the left-hand side of the constraints, and the vector b concatenates the right-hand side bᵢ, such that b = (b₀, b₁, · · ·, bₘ )ᵀ.

Also, as before, we concatenate the velocities of all the rigid bodies into one single vector u = (v₀ᵀ, v₁ᵀ, · · · , v_Kᵀ )ᵀ. Each row, Jᵢ, represents one constraint, and two consecutive columns J,₂ₖ,J,₂ₖ₊₁ represent the rigid body k. Each element bᵢ in b represents one RHS for the constraint i. Please note that each row in J is mostly empty (zero) except for two or four elements that correspond to the aᵢ,ₖ₀ and possibly aᵢ,ₖ₁.

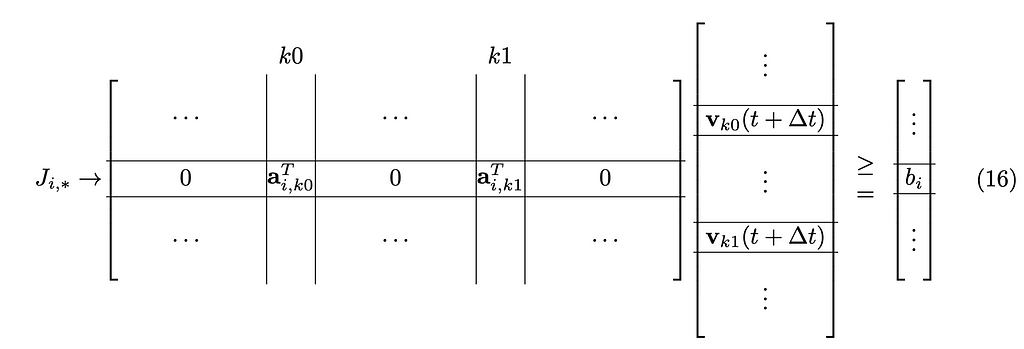
Now we can express all the constraints compactly by:

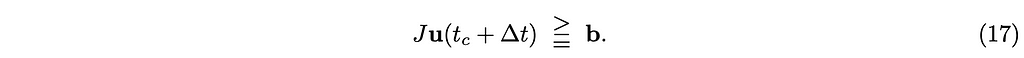
where the operator in the middle of (17) is a notational convenience that denotes that the upper part is for the unilateral (inequality) constraints and the lower part is for the bilateral (equality) constraints.

Construction of constraints

The next problem is how to express the constraints you want to apply in the velocity terms. After all, it is much more intuitive for us to express the constraints in positions. Please see Fig. 1.

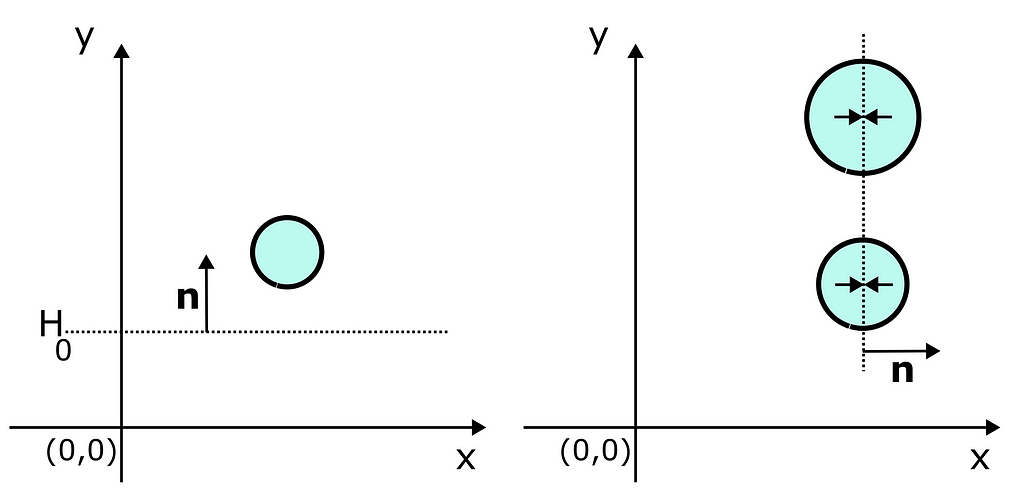
If the floor is placed at the height H₀, and if all the spherical rigid bodies must be above the floor, we can add a positional unilateral constraints such that yₖ (t + ∆t) >= H₀ + rₖ, where yₖ and rₖ are the vertical positions and the radius of the rigid body k respectively. If the horizontal position of two rigid bodies, k0 and k1, must be aligned at their centers, then we can add a bilateral positional constraint such that xₖ₀(t+∆t)−xₖ₁(t+∆t) = 0.

How can we convert those positional constraints into the velocity space? Unfortunately, it is not straightforward, and I’ll explain how to convert them in the next article. For now, let’s assume we already have constraints in the velocity space in this article.

Simulation Equations

So far, we have introduced two sets of rules for the velocities. One is from Newton’s second Law and the Euler method:

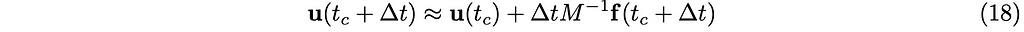
and the other one is the set of velocity-space constraints

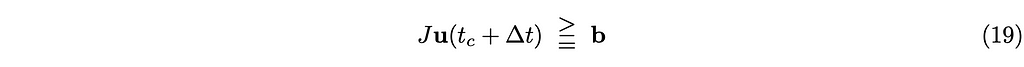
where M ∈ R²ᴷˣ²ᴷ is a diagonal matrix in which the mass of each rigid body is repeated twice as follows

and

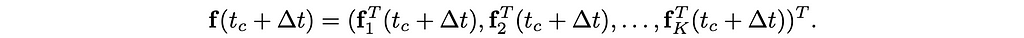
How can we combine those equations (18) and (19)? To put the conclusion first, equation (18) will be expanded to the following with the new term M⁻¹Jᵀ λ.

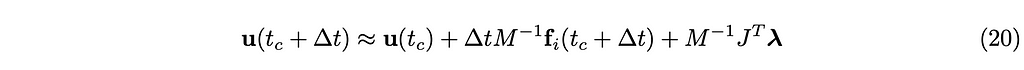
The new term M⁻¹Jᵀ λ is introduced to keep u(t_c+∆t) in the feasible region, and the vector λ ∈ Rᴺ is called the Lagrangian multiplier, where N is the number of constraints.

What’s the reason for the new term M⁻¹Jᵀ λ, and how to find λ? Before answering those questions, we have a more fundamental question:

Where should u(t_c+∆t) be after introducing the constraints?

It must satisfy all the constraints, i.e., it must reside in the feasible region. If there are only bilateral constraints, and there is no energy consumed or added to the system, we can use an argument called the principle of virtual work. In this case, the bilateral constraints are called Holonomic constraints, and the derivation of the new term with the Lagrangian is described in the literature, such as in Section 1.4 of the book Classical Mechanics Third Edition by Goldstein, Poole, & Safko [GPS01].

It is also often discussed in the simulation literature. However, this argument can not be applied to unilateral constraints in general, as the energy is often consumed during the simulation. For example, imagine an object falling onto a floor and it has come to rest on it after the collision is solved by a set of unilateral constraints that have absorbed the object’s kinetic energy. We need a different approach to the problem.

Anyway, let’s think about a simple situation as an example: an object is flying along a parabolic trajectory and eventually coming into contact with the floor. Please see Fig. 2, in which the rigid body comes into contact with the floor between t6 and t7.

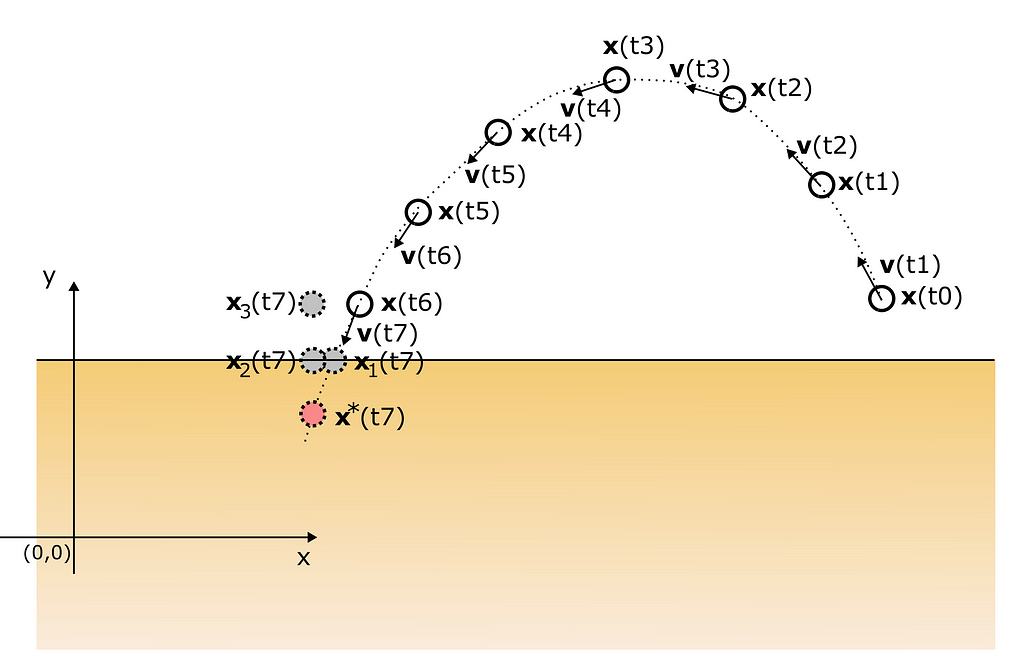
How should the collision be solved, and where should the object be positioned within the feasible region? Should that be x₁(t7), where the trajectory intersects with the floor plane? Or should that be x₃(t7) after a perfectly elastic bounce? Or somewhere else? In any case, how the velocity v(t7) be calculated? Let’s find one way of finding the location in the next section.

Minimizing the Change in the Total Momentum

Let u^∗(t_c+∆t) be the concatenated velocities of all the rigid bodies according to only Newton’s second law as if there were no constraints.

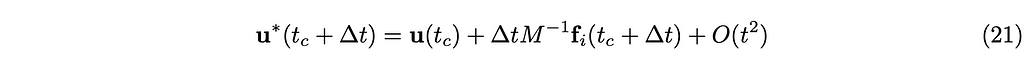
Let u(t_c+∆t) be the yet unknown velocity we try to find within the feasible region. And let the change in the concatenated momenta p of all the rigid bodies be defined as follows:

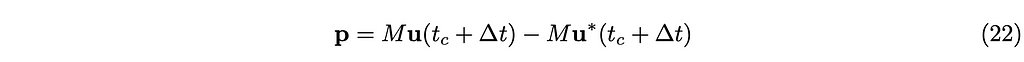
and its magnitude is:

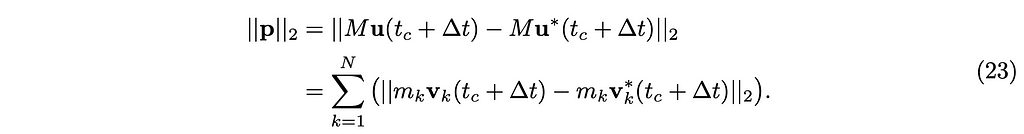
The p is the concatenated set of impulses required to correct the velocity from u^∗(t_c+∆t) to u(t_c+∆t). We want to find a p of the minimum magnitude, i.e. we want to find the smallest set of impulses, just enough to bring u(t_c + ∆t) into the feasible region.

Then we can model the problem of finding u(t_c + ∆t) as the following constraint minimization problem.

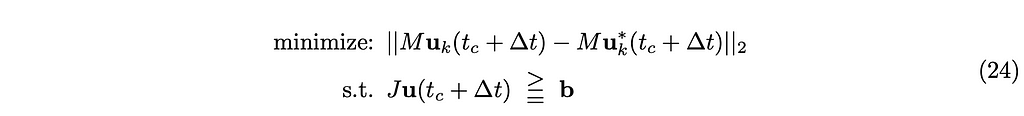
or in an equivalent but more tractable form:

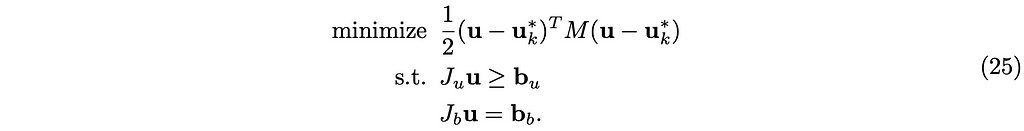
where (t_c+∆t) is omitted for clarity, and Jᵤ and J_b are the unilateral and bilateral part of J, respectively such that

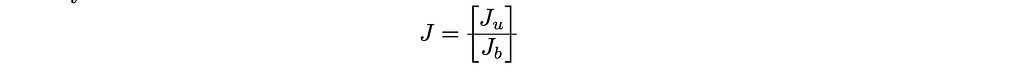
and in the same way,

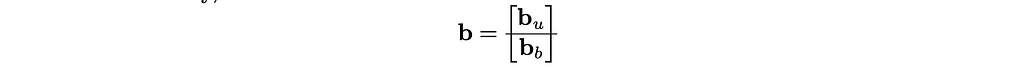
This (25) is a constrained convex (quadratic) optimization problem, which can be solved by a Lagrangian as follows.

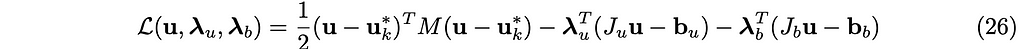
By taking the derivatives of this Lagrangian, we can derive the following equations:

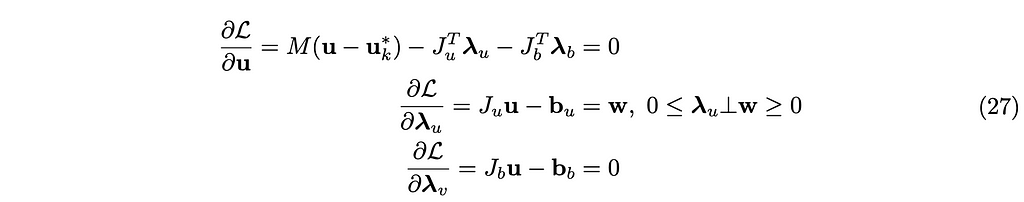
The new variable w is called the slack variable, which is paired with λᵤ. With the slack variable, the unilateral constraints can be expressed by Jᵤu − bᵤ = w, w ≥ 0. The Lagrangian multiplier for the unilateral constraints λᵤ must be non-negative. Also, for each element λᵢ ∈ λᵤ, and the corresponding element in the slack variable wᵢ ∈ w, only one of two is allowed to be strictly positive, i.e., λᵢwᵢ = 0.

This is called the complementarity condition, compactly denoted by 0 ≤ λᵤ⊥w ≥ 0. The reason for the complementarity condition is explained with the active/inactive argument in Appendix 4. Optimality Conditions for Smooth Optimization Problems in [MY97]. You can read this part independently from the rest of the book.

From the first partial differential equation in (27), the following is derived:

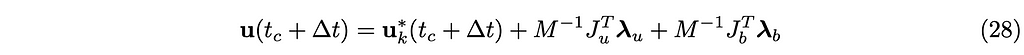
Substitute u^∗(t_c+∆t) in (28) with (21),

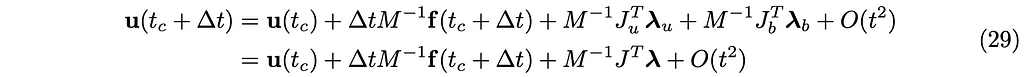
where

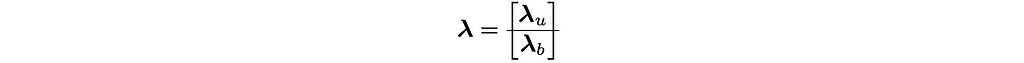
This is what we wanted to derive. The reason why we form the Lagrangian for the constrained minimization problem and how to derive those equations is best explained in Appendix 4 of Murty’s book [MY97]. I would recommend you read through the chapter once.

In this section, we have covered the reason for the new term J ᵀλ. Let’s try to find λ in the next section.

Solving λ with MLCP

Now, let’s find λ. Let’s see what we have now. From equation (29),

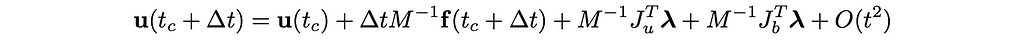
and from the second and third equations in (27),

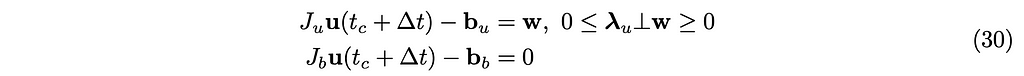
We want to eliminate u(t_c+∆t). For that, we substitute u(t_c+∆t) in the two constraints (30) with equation (29) as follows:

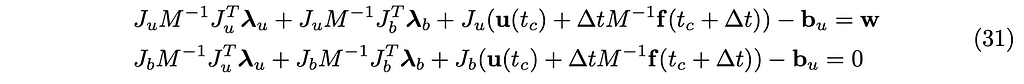
Let’s join those two into a more compact notation:

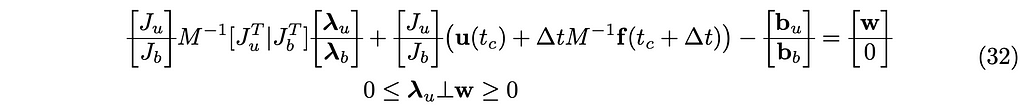
Let

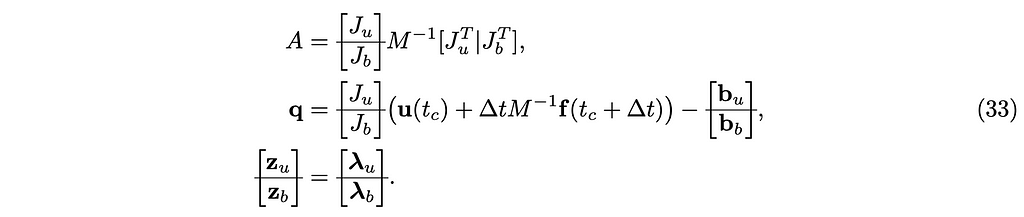
Then we found the following mixed linear complementarity problem or MLCP.

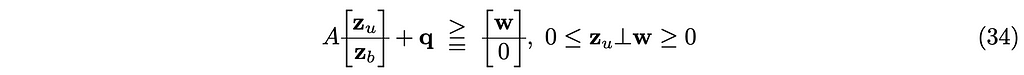
Since the entries of the diagonal matrix M⁻¹ are all positive, A is a PD matrix, and an iterative solver can be used. One of the most commonly used is called projected Gauss-Seidel. Later, when we start treating frictions with friction cones, we have to augment the matrix A with the friction cones, making the A non-symmetric. The Gauss-Seidel-based iterative solvers can not be used for non-symmetric matrices, and a pivot-based solver, notably Lemke solver should be used. (It’s not clear to me if any of the fixed-point iterative methods can be used for this type of matrices.

Chap 9 of [MY97] discusses the conditions in which the solution by the iterative solvers converge, but it’s unclear to me if any of those cases can be applied to A. According to my experiments using some real data with hexagonal frictional cones, the solutions by the PGS solver did not converge. So for non-symmetric matrices, using a pivot-based solver is safe.) However, the pivot-based algorithms can solve only LCP problems, i.e., problems with only inequality constraints. In this case, we will have to decompose A and eliminate z_b by the Schur complement.

Let’s decompose the equation (34) by partitioning it into the unilateral and bilateral components as follows.

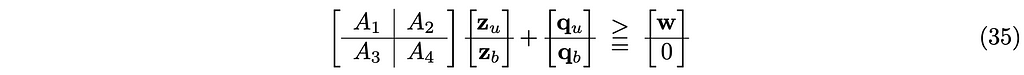
and separate it into two:

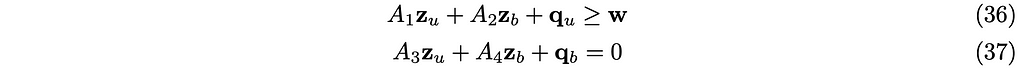
From the equation (37),

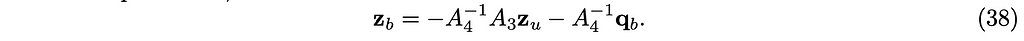
Substitute z_b in the equation (36) with equation (38) to

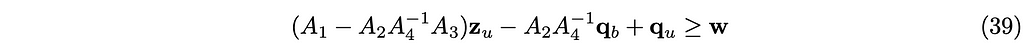
This is a pure LCP problem for zᵤ, which can be solved by the Lemke solver. The inverse of A₄ is usually found by Cholesky factorization, which may become costly if A₄ is large. After zᵤ is found, we can find z_b by equation (38), and then we can advance the simulation for the time step t+∆t with equation (29).

If you want to use an iterative solver with friction, i.e., if you want to keep the matrix A PD and want to handle friction, then something called boxed constraint can be used, which will be described in a future article. Or you can read 1.7 The Boxed Linear Complementarity Problem Model in SIGRAPH’22 Course Notes.

Recap on Theory

So far, we have covered the core idea of the velocity-space constraint-based rigid body simulation. Let’s recap what we have discussed. The physics engine finds the velocities at the next time step based on a numerical integration of Newton-Euler’s second law and on the constraints. To handle the constraints, we have modeled the problem as a minimization of the total momentum to correct the velocities such that they stay in the feasible region.

The Lagrangian is formed as a constrained quadratic optimization problem, then transformed into the mixed linear complementarity problem. The MLCP problem is solved by mainly two types of solvers: PGS (iterative) and Lemke (pivot).

In an actual implementation, one iteration for the time step t_c+∆t can consist of the following steps:

Find the force fₖ for each rigid body k.
Update u^∗(t_c+∆t) and x^∗(t_c+∆t) from Newton-Euler second law with the Euler step.
Run collision detection to find contact pairs based on u^∗(t_c+∆t) and x^∗(t_c+∆t).
Construct unilateral and bilateral constraints in J and b for the contact pairs and the joints.
From J, b, and u^∗(t_c+∆t), form an MLCP into Az+q=[w|0]ᵀ
Solve the MLCP for z, i.e., λ.
Update u(t_c+∆t) and x(t_c+∆t) from Newton-Euler’s second law with the Euler step with the induced impulses Jᵀ λ.

Sample Program

[Link to video]

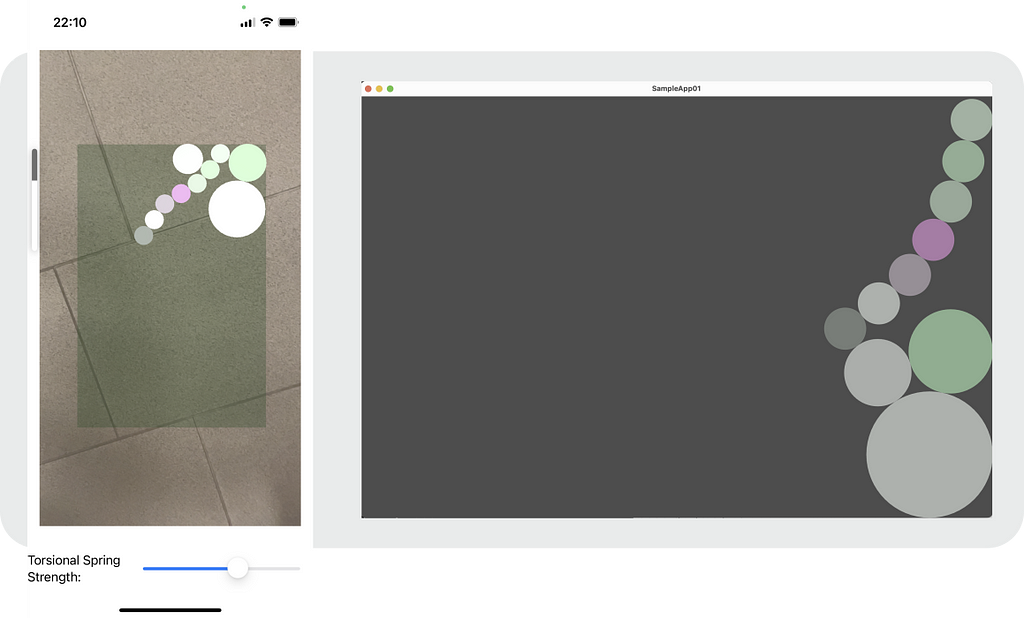
Now, let the fun part begin. Grab the code for the sample programs from my GitHub repo. It comes in two types: a command line OpenGL program for Linux (including MacOS with no guarantee) and an AR App for iOS.

The program shows ten discs confined in a rectangular region. They roll around based on Newton’s second law. For the discs to avoid collisions against each other and the walls, unilateral constraints are applied. The seven small discs are linked together to form a chain. A set of bilateral constraints realizes the chain. There are two types of forces applied to each disc. One is the gravity which is controlled by the iOS device’s tilt or the mouse cursor’s location relative to the center of the screen. The other is the torsional forces applied to the seven chained discs. Those forces make a pool noodle like behavior for the chained discs.

Build and Run

iOS

For iOS, open SampleApp01/SampleApp01.xcodeproj with XCode, plug an iOS device in, build and run. It’s an AR App. After opening the App, hold it steady for a short while to let AR calibrate itself. You will get a screen with a camera image and ten superimposed discs. Tilt the device to let the discs roll with gravity. The slider below controls the strength of the torsional forces applied to the seven small discs chained together. I tested it with iPhone 13 mini & iOS 16.6 on Mac mini M1, 2020 Ventura 13.5, and XCode 14.3.1.

Linux

For Linux, open a terminal, go to SampleApp01/SampleApp01/LinuxOpenGL and follow the usual CMake process.

$ cd <path/to>/SampleApp01/SampleApp01/LinuxOpenGL
$ mkdir build
$ cd build
$ cmake ..
$ make VERBOS3E=1
$ ./sample_app_01

You need to have GLEW, GLFW, and GLM installed on the machine (and lots of dependent packages), usually installed by the package manager. For Ubuntu, I tested it with Ubuntu 22.04.3 on Intel Core i5 and Intel 640. See the README in the repo.

Notes on macOS: It also works on my Mac (Mac mini M1, 2020, Ventura 13.5), but it may be a bit tricky to get it up and running. OpenGL is no longer officially supported, and you may encounter some problems around GLFW. CMakeLists.txt is configured to use a locally-built GLFW for macOS.

Start the command ./sample app 01. A window will pop up with ten discs in it. The forces are applied to the discs according to the cursor’s location relative to the center of the screen. The forces depend on the direction and the distance from the center of the screen. Arrow keys control the strength of the torsional forces applied to the seven small discs chained together. The current strength is printed to the console. ‘Up’ and ‘Left’ increases the forces, and ‘Down’ and ‘Right’ decreases it.

Code overview

Now, let’s take a look at the code briefly. In this article, we will briefly examine the code organization relevant to the rigid body simulation and one function corresponding to one step of the physics simulation.

The iOS App and the Linux program share the same code for the simulation. They are found in SampleApp01/SampleApp01/Simulation. It contains two C++ header files and a directory, which in turn contains seven small C++ header files as follows.

/SampleApp01/Simulation
    Simlator.hpp
    ChainedDisc.hpp
    Common/
        Vec2.hpp
        Vec3.hpp
        Vec4.hpp
        RigidBody.hpp
        VelocityConstraint.hpp
        ConstraintSolver.hpp
        MLCPSolverVanillaPGS.hpp

Simulator is the top-level class that constructs the discs and advances the simulation at each time step.
ChainedDisc represents one disc. It is a subclass of RigidBody.
RigidBody represents one rigid body. It holds the position, velocity, forces, etc., and it is responsible for the physics behavior.
VelocityConstraint holds all the data necessary for one unilateral or bilateral constraint.
ConstraintSolver receives the VelocityConstraints and solves them for λ.
MLCPSolverVanillaPGS is an iterative MLCP solver invoked by ConstraintSolver.

The most important part of the code for this article is the following in Simulator to advance the simulation for a time step. The function’s body is annotated with the items in Recap on Theory above so that you can check which part of the code corresponds to which step above:

    void  Simulator::update( const float delta_t, const Vec2& accel, float torsional_spring_strength )
    {
        updateAreaSize();

        // "Find the forces f_k for each rigid body k"
        for ( auto* disc : m_discs ) {

            disc->resetForcesAndImpulses();
            disc->accumulateForce( accel * disc->m_mass * G );
            addTorsionalSpringForce( disc, torsional_spring_strength );
        }

        // "Update u^*(tc + t) and x^*(tc + t) from Newton-Euler 2nd Law with the Euler step."
        for ( auto* disc : m_discs ) {

            disc->updatePhaseSpaceTmp( delta_t );
        }

        // "Run collision detection to find contact pairs."
        detectCollisions( delta_t );

        constructBilateralConstraints( delta_t );

        // "Construct unilateral and bilateral constraints in J and b for the contact pairs and the joints."

        // "From J, b, and u^*(tc + t), form an MLCP into Az+q=[w|0]."
        m_constraints_solver.reset();
        for ( auto* c : m_constraints ) {

            m_constraints_solver.add( c );
        }

        // "Solve the MLCP for z, i.e., lambda"
        m_constraints_solver.run( delta_t );

        for ( auto* c : m_constraints ) {

            if ( c->m_body_0 != nullptr ) {
                 c->m_body_0->addImpulse( c->m_n0 * c->m_lambda );
            }

            if ( c->m_body_1 != nullptr ) {
                 c->m_body_1->addImpulse( c->m_n1 * c->m_lambda );
            }
            delete c;
        }
        m_constraints.clear();

        // "Update u(tc + t) and x(tc + t) from Newton-Euler 2nd Law with the Euler step with the induced impulses J^Tlambda"
        for ( auto* disc : m_discs ) {

            disc->updatePhaseSpace( delta_t );
        }
    }

The code in Simulator and under it is pretty small, with just over 1,000 lines of code, and it would not be too much hustle to read them through. Anyway, that’s pretty much about it for this article. Let’s dig deeper into the parts for the velocity-space constraints in the next article.

Conclusion

In this article, we have covered the core idea of the ‘velocity-space constraint-based rigid body simulation’ from the theory to the working implementation in C++. We have not covered how to construct the velocity-space constraints, which will be the main topic of the next article. I hope you enjoyed this article and the program and have a rough idea of what’s happening inside a rigid-body physics engine.

Happy programming.