Students seeing differential equations for the first time expect every equation to have a nice closed-form solution, because up to that point in their education nearly every problem they’ve seen has been contrived to have a nice closed-form solution.

Once you resign yourself to the fact that a differential equation will rarely have a closed form solution, it’s a treat when you run across one that does. This is especially true for nonlinear equations.

The Korteweg–De Vries (KdV) equation is

u_t - 6 u, u_x + u_{xxx} = 0

is such a treat. I wrote a few days ago about the sech² solution to the KdV equation.

u(x,t) = -frac{v}{2} ,text{sech}^2left(frac{sqrt{v}}{2} (x - vt - a)right )

There’s also a rational solution:

u(x, t) = 6 x frac{ left(x^3-24 tright)}{left(x^3 + 12 tright)^2}

We can verify this is a solution to the KdV equation reusing the Mathematica code from the earlier post.

    u[x_, t_] := u[x_, t_] := 6 x (x^3 - 24 t)/(x^3 + 12 t)^2
    Simplify[ D[u[x, t], {t, 1}] 
            - 6 u[x, t] D[u[x, t], {x, 1}] 
            + D[u[x, t], {x, 3}] ]

This simplifies to 0.

Here’s a plot:

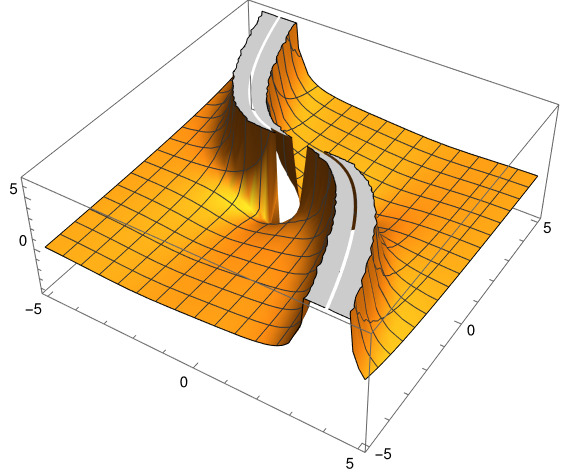
The top of the plot looks like a two-lane road on top of a mountain ridge, with a sinkhole in the middle of the road.

The “road” is a artifact of plotting. The solution is singular along the curve x³ + 12t= 0, and Mathematica had to chop the top of the graph off because it can’t plot an infinitely tall function.

 

The post Rational solution to Korteweg–De Vries equation first appeared on John D. Cook.

Previous Post
Next Post