Yesterday’s post looked at the distribution of powers of x mod 1. For almost all x > 1 the distribution is uniform in the limit. But there are exceptions, and the post raised the question of whether 3 + √2 is an exception.

A plot made it look like 3 + √2 is an exception, but that turned out to be a numerical problem.

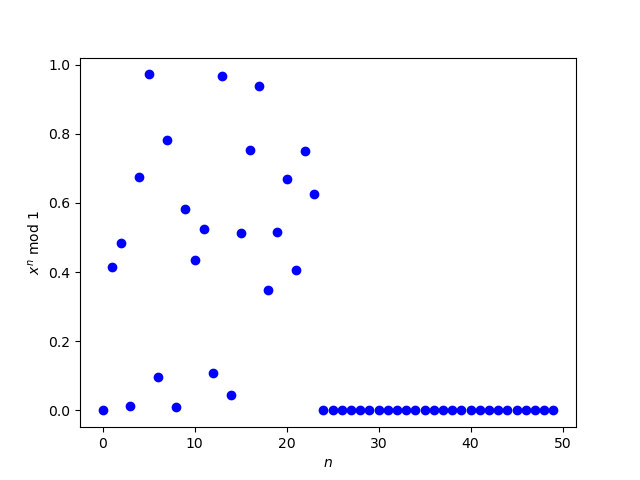
A higher precision calculation showed that the zeros on the right end of the plot were erroneous.

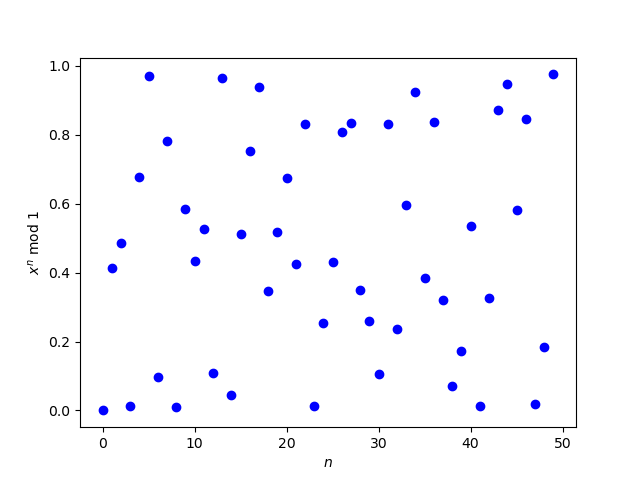
So this raises the question of how to calculate (3 + √2)ⁿ accurately for large n. The way I created the second plot was to use bc to numerically calculate the powers of 3 + √2. In this post, I’ll look at using Mathematica to calculate the powers symbolically.

For all positive integers n,

(3 + √2)ⁿ = a_n + b_n√2

where a_n and b_n are positive integers. We want to compute the a and b values.

If you ask Mathematica to compute (3 + √2)ⁿ it will simply echo the expression. But if you use the Expand function it will give you want you want. For example

    Expand[(3 + Sqrt[2])^10]

returns

    1404491 + 993054 √2

We can use the Coefficient function to split a + b √2 into a and b.

    parts[n_] := 
        Module[{x = (3 + Sqrt[2])^n}, 
            {Coefficient[x, Sqrt[2], 0], Coefficient[x, Sqrt[2], 1]}]

Now parts[10] returns the pair {1404491, 993054}.

Here’s something interesting. If we set

(3 + √2)ⁿ = a_n + b_n√2

as above, then the two halves of the expression on the right are asymptotically equal. That is, as n goes to infinity, the ratio

a_n /  b_n√2

converges to 1.

We can see this by defining

    ratio[n_] := 
        Module[ {a = Part[ parts[n], 1], b = Part[parts[n], 2]}, 
        N[a / (b Sqrt[2])]]

and evaluating ratio at increasing values of n. ratio[12] returns 1.00001 and ratio[13] returns 1, not that the ratio is exactly 1, but it is as close to 1 as a floating point number can represent.

This seems to be true more generally, as we can investigate with the following function.

    ratio2[p_, q_, r_, n_] := 
        Module[{x = (p + q Sqrt[r])^n}, 
            N[Coefficient[x, Sqrt[r], 0]/(Coefficient[x, Sqrt[r], 1] Sqrt[r])]]

When r is a prime and

(p + q√r)ⁿ = a_n + b_n√r

then it seems that the ratio a_n / b_n √r converges to 1 as n goes to infinity. For example, ratio2[3, 5, 11, 40] returns 1, meaning that the two halves of the expression for (3 + 5√11)ⁿ are asymptotically equal.

I don’t know whether the suggested result is true, or how to prove it if it is true. Feels like a result from algebraic number theory, which is not something I know much about.

Update: An anonymous person on X suggested a clever and simple proof. Observe that

In this form it’s clear that the ratio a_n / b_n √2 converges to 1, and the proof can be generalized to cover more.

The post Powers of 3 + √2 first appeared on John D. Cook.