Stefan Steinerberger defines “an amusing sequence of functions” in [1] by

Here’s a plot of f₃₀(x):

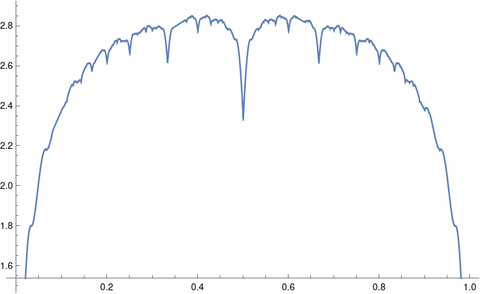
As you can see, f_n(x) has a lot of local minima, and the number of local minima increases rapidly with n.

Here’s a naive attempt to produce the plot above using Python.

    from numpy import sin, pi, linspace
    import matplotlib.pyplot as plt

    def f(x, n):
        return sum( abs(sin(k*pi*x))/k  for k in range(1, n+1) )

    x = linspace(0, 1)
    plt.show()

This produces the following.

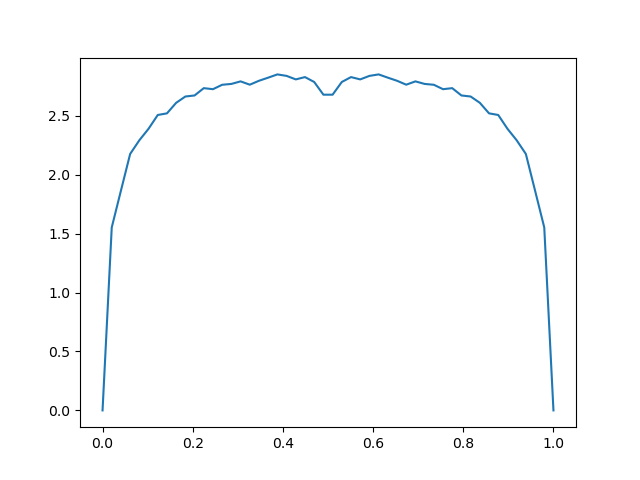
The code above doesn’t specify how finely to divide the interval [0, 1], and by default linspace will produce 50 evenly spaced points. In the example above we need a lot more points. But how many? This is not a simple question.

You could try more points, adding a third argument to linspace, say 1000. That will produce something that looks more like the first plot, but is the first plot right?

The first plot was produced by the Mathematica statements

    f[x_, n_] := Sum[Abs[Sin[Pi k x]/k], {k, 1, n}]
    Plot[f[x, 30], {x, 0, 1}]

Mathematica adaptively determines how many plotting points to use. It tries to detect when a function is changing rapidly in some region and allocate more points there. The function that is the subject of this post makes a good test case for such automated refinement.

Often Mathematica does a good enough job automatically, but sometimes it needs help. The Plot function takes additional parameters like PlotPoints and MaxRecursion that you can use to tell Mathematica to work harder.

It would be an interesting exercise to make a high quality plot of f_n for some moderately large n, making sure you’ve captured all the local minima.

[1] Stefan Steinerberger. An Amusing Sequence of Functions. Mathematics Magazine, Vol. 91, No. 4 (October 2018), pp. 262–266

The post Plotting a function with a lot of local minima first appeared on John D. Cook.