The previous post looked at a function formed by patching together the function
f(x) = log(1 + x)
for positive x and
f(x) = x
for negative x. The functions have a mediocre fit, which may be adequate for some applications, such as plotting data points, but not for others, such as visual design. Here’s a plot.
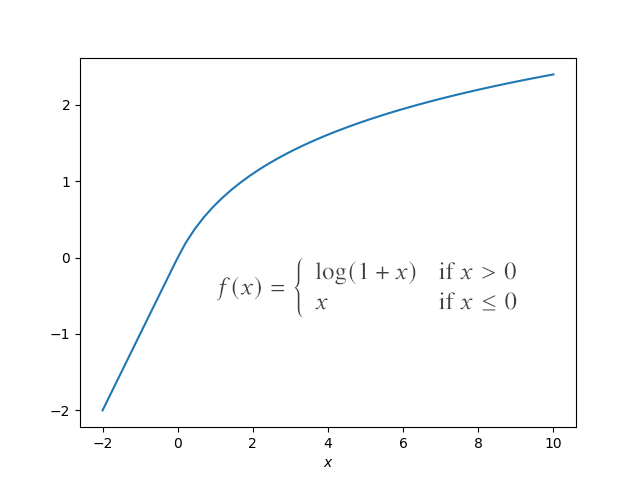
There’s something not quite smooth about the plot. It’s continuous, even differentiable, at 0, but still there’s sort of a kink at 0.
The way to quantify smoothness is to count how many times you can differentiate a function and have a continuous result. We would say the function above is C¹ but not C² because its first derivative is continuous but not differentiable. If two functions have the same number of derivatives, you can distinguish their smoothness by looking at the size of the derivatives. Or if you really want to get sophisticated, you can use Sobolev norms.
As a rule of thumb, your vision can detect a discontinuity in the second derivative, maybe the third derivative in some particularly sensitive contexts. For physical applications, you also want continuous second derivatives (acceleration). For example, you want a roller coaster track to be more than just continuous and once differentiable.
Natural cubic splines are often used in applications because they patch cubic polynomials together so that the result is C².
You can patch together smooth functions somewhat arbitrarily, but not analytic functions. If you wanted to extend the function log(1 + x) analytically, your only choice is log(1 + x). More on that here.
If you patch together a flat line and a circle, as in the corners of a rounded rectangle, the curve is continuous but not C². The second derivative jumps from 0 to 1/r where r is the radius of the circle. A squircle is similar to a rounded rectangle but has smoothly varying curvature.
Related posts
The post Patching functions together first appeared on John D. Cook.