The previous post mentioned Newton’s inequality. This post will explore this inequality.

Let x be a list of real numbers and define S_n(x) to be the average over all products of n elements from x. Newton’s inequality says that

S_n−1 S_n+1 ≤ S²_n

In more terminology more recent than Newton, we say that the sequence S_n is log-concave.

The name comes from the fact that if the elements of x are positive, and hence the S‘s are positive, we can take the logarithm of both sides of the inequality and have

(log S_n−1 + log S_n+1)/2 ≤ log S_n

which is the discrete analog of saying log S_k is concave as a function of k.

Let’s illustrate this with some Python code.

from itertools import combinations as C
from numpy import random
from math import comb
import matplotlib.pyplot as plt

def S(x, n):
    p = lambda c: prod([t for t in c])
    return sum(p(c) for c in C(x, n))/comb(N, n)

random.seed(20231010)
N = 10
xs = random.random(N)
ns = range(1, N+1)
ys = [log(S(xs, n)) for n in ns]

plt.plot(ns, ys, 'o')
plt.xlabel(r"$n$")
plt.ylabel(r"$log S_n$")
plt.show()

This produces the following plot.

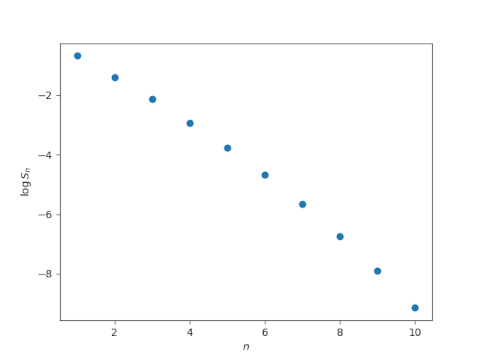
This plot looks nearly linear. It’s plausible that it’s concave.

The post Newton’s inequality and log concave sequences first appeared on John D. Cook.