Since the release of NeRF at ECCV 2020 there’s been more and more NeRF papers published each year. This trend continued at CVPR 2023, where 5% of the total papers, i.e. around 120 papers, revolved around NeRF and its various iterations! Let’s have a look at two papers about Arbitrary Camera Trajectories

In this article, I’ll detail two NeRF articles dealing with Arbitrary Camera Trajectories that caught my attention during the CVPR 2023 conference.
Please note that the selection I have compiled is highly subjective, and I want to emphasize that it was a challenging task to choose only two of them. Explaining too many papers in the same article could overwhelm the reader. As a result, I regretfully had to exclude notable papers, despite their substantial contributions in the field.
I’m assuming that you’re already familiar with NeRF. If not, I recommend referring to my Medium article on the subject for an introduction to NeRF (5 things you must know about Neural radiance fields ⚡).
0. Introduction
Insights
Prior to delving into the details of these two papers, I’d like to provide some insights into their shared motivations.
Grid-based methods, such as Instant-NGP, TensoRF or Plenoxels, can’t have an infinite number of voxels since they have to be stored in memory. Consequently, the 3D scene must be somehow pre-processed to fit into a finite feature-grid.
Naively, we could think that this problem doesn’t concern the original NeRF since it directly feeds the continuous coordinates into a MLP. But it does because of the positional encoding! If the difference between two 3D points is a multiple of 2π along each axis, then the points will have the exact same positional encoding. In other words, a NeRF model exhibits a periodicity of 2π, and we must make the scene fit into [-π,π]³.
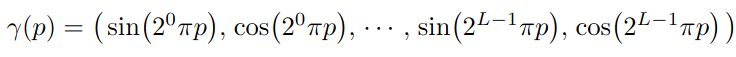
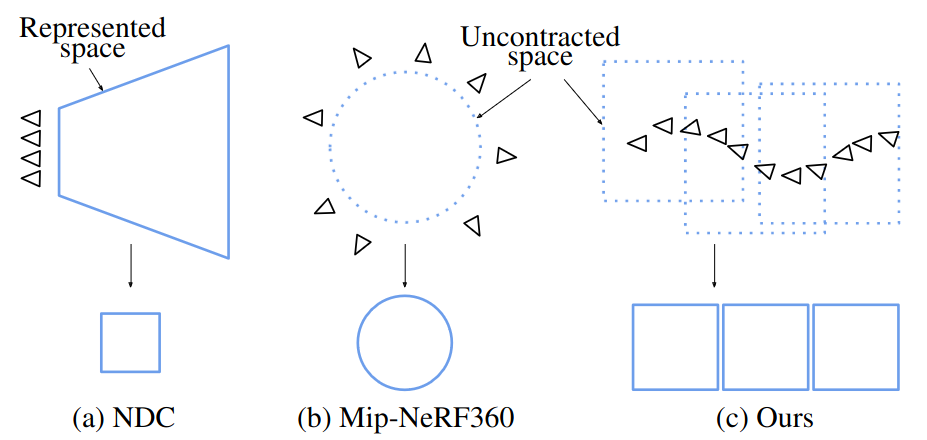
As we’ll see later, everything outside the unit cube isn’t necessarily ignored. For instance, unbounded scene can be mapped to a bounded one by contracting on each axis the range [1,+∞[ to [1,2]. Each NeRF architecture has its own way of allocating representational capacity in the scene. Therefore, it’s always crucial to understand how the scene is positioned with respect to the unit cube or the unit sphere.
Script colmap2nerf.py
Instant NGP provides a “colmap2nerf.py” script that runs COLMAP and preprocesses the resulting camera poses. It works well and most people probably haven’t bothered to look at what it’s actually doing. Essentially, the script centers the scene around the average intersection point of the camera optical axes and scales the scene to ensure that the average distance from the cameras to the origin is 4.
As illustrated in the screenshot below, this normalization makes perfect sense when the cameras are all pointing at the same object in the center of the scene and are roughly at the same distance from the object. In other words, when the camera poses are positioned on a sphere/hemisphere and directed towards the origin.

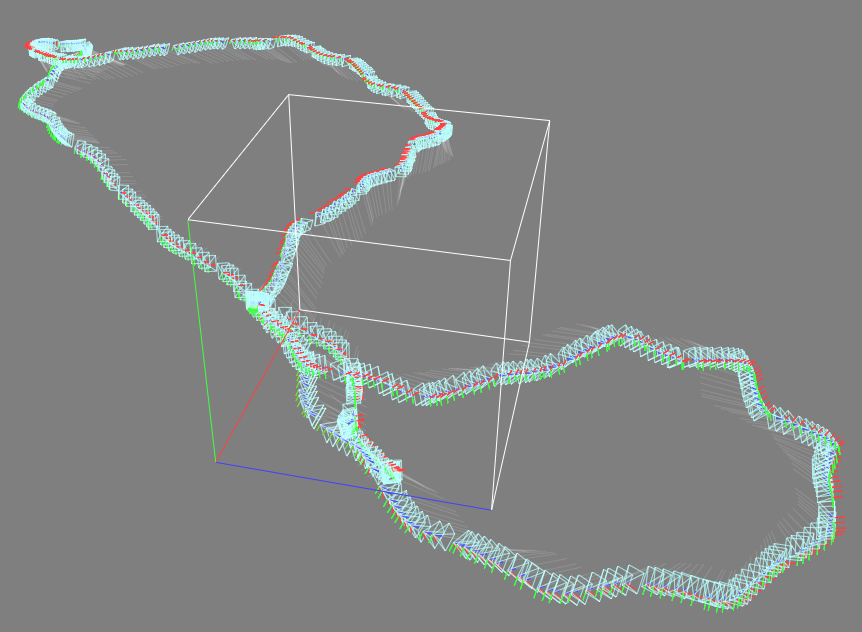
However, when the cameras start to point in different directions, the average intersection of the camera’s optical axes becomes entirely arbitrary. So does the scaling. The cameras in the image below were captured while walking back and forth inside a rectangular room, carefully avoiding any tables or chairs. When blindly utilizing “colmap2nerf.py”, as can be observed, a large part of the scene happens to lie outside the unit cube, which degrades the performance.
Datasets
Despite the diversity in object appearance, most of the publicly available NeRF datasets share a common aspect: the camera either moves around an object or remains forward-facing, focusing on the object.
Having access solely to these specific cases restricts the ability to estimate the accuracy that a given NeRF architecture could achieve on a generic camera trajectory with multiple points of interest.


1. F2-NeRF
Fast Neural Radiance Field Training with Free Camera Trajectories
(Peng Wang, Yuan Liu, Zhaoxi Chen, Lingjie Liu,
Ziwei Liu, Taku Komura, Christian Theobalt, Wenping Wang)
Space Warping
As mentioned earlier, current fast grid-based NeRF architectures are primarily tailored for bounded scenes and rely on space warping to handle unbounded scenes. The diagrams below are pretty intuitive.
- Normalized Device Coordinates Warping (NDC):
Project the points using a Pinhole Camera and contract the depth from [znear, +∞[ to [-1,1] - Inverse Sphere Warping:
Keep the unit ball unchanged, but contract everything outside the unit ball to fit within a ball with a radius of 2.
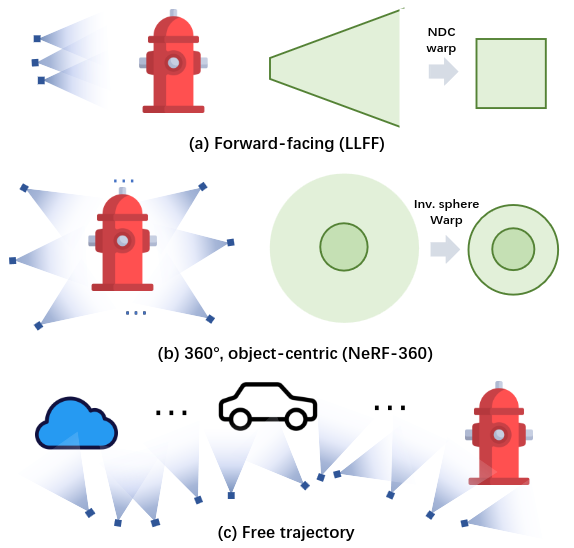
Unfortunately, there’s no intuitive space warping designed for an arbitrary camera trajectories with multiple objects of interest.
Applying the inverse sphere mapping would indeed make any free trajectory bounded. However, it would lead to an uneven allocation of spatial representation capacity: wasted on empty space and with insufficient details in areas of interest.
Perspective Warping
F2-NeRF introduced a new generic space warping function called Perspective Warping, which turns out to be a generalization of both the Inverse Sphere and the NDC sampling.
Intuitively, dense grids should be allocated for foreground objects to preserve intricate shape details, while coarse grids should be assigned to background space. Yet, the distinction between foreground and background may vary across the scene due to the cameras not being solely forward-facing or object-centric.
We start to feel that the quality of being a good warping function is local and relies on the specific subset of cameras being utilized.
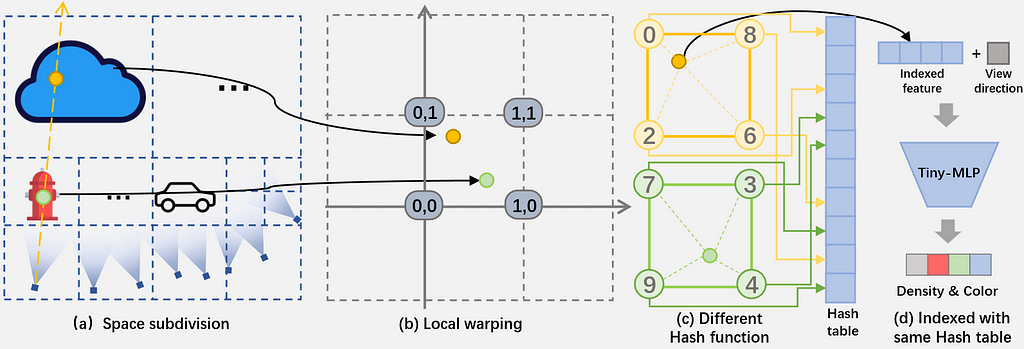
As illustrated in the diagram below, F2-NeRF starts by subdividing the space into regions, where we can establish a meaningful distinction between foreground and background on a local level by using a fixed set of cameras. Starting with a bounding box 512 times larger than the box containing the cameras, we iteratively subdivide using a split criterion. Finally, each subdivision selects at most 4 reference visible cameras and defines the corresponding warping function, which will be described in the next section.
Hash conflicts are solved by using a different hash function per subdivision. That way, two points from different regions ending up at the same location in the local warping space won’t have the same features. It’s like using Instant-NGP but with a warping specifically tailored for free-trajectories.
It is important to understand that the subdivision grid is not the feature grid; rather, it serves as a coarse grid that defines local warping functions.
Details of the Perspective warping Function
Given a set of reference cameras looking at a subdivision, we’d like to give more representational power to the foreground points. This can be done by using the perspective, like in NDC and Inverse Sphere warpings, to project a point onto the image plane of each of the n reference cameras. The resulting 2D points are then concatenated into a vector of length 2n. This mapping however isn’t particularly helpful since we want to map 3D points back to the 3D space.
A hack introduced by F2-NeRF is to regularly sample the subdivision region in 3D, compute the 2n aggregated projection vector and perform a PCA to extract the 3 most meaningful axes. This gives us a projection matrix of shape 3x2n, that can be pre-computed once the subdivision space has been defined, and maps the projections back to 3D. So we do have a 3D point!
Free Dataset
They introduced a new dataset of 7 free trajectories, consisting in long and narrow trajectories with multiple foreground objects in focus.

2. LocalRF
Progressively Optimized Local Radiance Fields for Robust View Synthesis
(Andreas Meuleman, Yu-Lun Liu, Chen Gao, Jia-Bin Huang, Changil Kim, Min H. Kim, Johannes Kopf)
Multiple local NeRFs along the camera trajectory
At first glance, while looking at their demo videos showcasing arbitrary trajectories, we might think that LocalRF and F2-NeRF are tackling the same problem. However, their goals are quite different.

On the one hand, F2-NeRF aims to get the most out of a fixed memory size by smartly allocating representational capacity within the scene.
On the other hand, LocalRF uses a dynamic allocation approach to generate new local radiance fields along the path. To ensure seamless transitions, these local NeRFs are blended together when rendering in overlapping regions. While this guarantees sharp details throughout the scene, it does come with the trade-off of requiring a larger memory footprint.
However, it is important to note that the RAM usage remains bounded as LocalRF optimizes one NeRF at a time.
Space Warping
The diagram below may look familiar to you, as it recaps the NDC and Mip-NeRF360 warpings mentioned in F2-NeRF. On the right, LocalRF uses a cubic version of the inverse sphere sampling technique from Mip-NeRF360 for each local NeRF.
LocalRF uses TensoRF for its local NeRFs due to its efficient training speed and compact model size. To optimize memory efficiency, the scene is compacted into a cube instead of a sphere, avoiding empty corner areas due to TensoRF’s dense 4D tensor storage.
Pose estimation
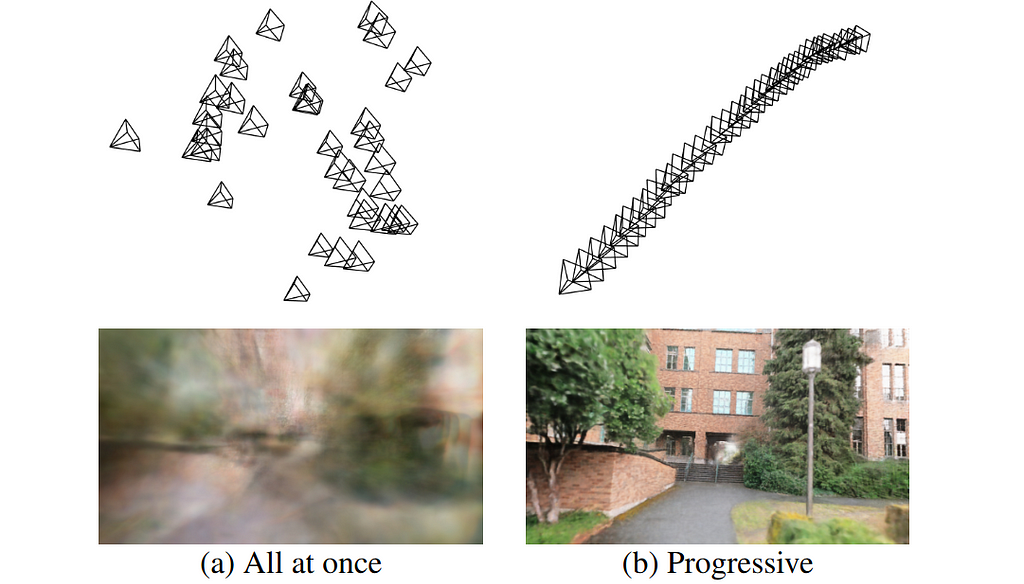
Furthermore, LocalRF optimizes both the local NeRFS and camera poses together. This is beneficial for handling challenging hand-held videos that standard SfM pipelines struggle with. The optimization process progressively incorporates frames to leverage temporal consistency.
Other methods, like BARF (Bundle-Adjusting NeRF) and NeRF– (NeRF Without Known Camera Parameters), have also tried to eliminate the need for known camera poses. However, these techniques struggle with long hand-held sequences and can get stuck in local minima.
LocalRF, on the other hand, excels by leveraging temporal consistency and gradually optimizing poses along the path, as shown in the images below.
Robustness
While it could be argued that without loop closure, there might be some drift along the trajectory, it becomes irrelevant if our objective is merely to stabilize the recorded video and render it along a smoothed version of the camera trajectory.
LocalRF is highly robust because the influence of inaccurate camera pose estimations is locally bounded. This means that an outlier pose will quickly be forgotten and will not ruin the quality of the entire scene.
Limitations
Estimating camera poses comes with a cost, requiring approximately 30–40 hours of training.
Moreover, each local NeRF has currently as many parameters as a standard TensoRF model, which results in a scene with a heavy memory footprint of a few gigabytes. Since they’re only local NeRFs, we could reduce their model size.
Static Hikes Dataset
Similar to F2-NeRF, they introduced a new dataset specifically addressing the challenge of very long hand-held videos capturing large-scale scenes. This was done to overcome the limitations in terms of scene variety present in existing NeRF datasets.

Conclusion
I hope you enjoyed reading this article and that it gave you more insights on NeRF!
See more of my code on GitHub.
NeRF at CVPR23: Arbitrary Camera Trajectories ➿ was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.