A Möbius transformation is a function of the form
where ad – bc = 1.
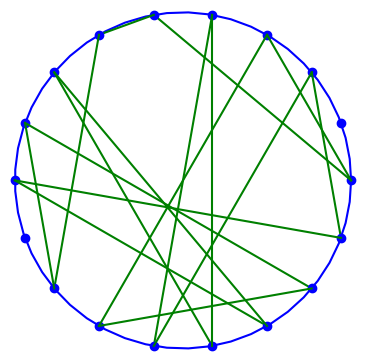
We usually think of z as a complex number, but it doesn’t have to be. We could define Möbius transformations in any context where we can multiply, add, and divide, i.e. over any field. In particular, we could work over a finite field such as the integers modulo a prime. The plot above represents a Möbius transformation over a finite field which we will describe below.
There is a subtle point, however. In the context of the complex numbers, the transformation above doesn’t quite map the complex plane onto the complex plane. It maps the complex plane minus one point to the complex plane minus one point. The domain is missing the point z = −d/c because that value makes the denominator zero. It’s also missing a point in the range, namely a/c.
The holes in the domain and range are a minor irritant, analogous to the pea in The Princess and the Pea. You can work around the holes, though the formalism is a little complicated. But over a finite field, the holes are a big deal. If you’re working over the integers mod 7, for example, then 1/7th of your domain is missing.
In the case of the complex numbers, the usual fix is to replace the complex numbers ℂ with the extended complex numbers ℂ ∪ ∞ and say that g(−d/c) = ∞ and g(∞) = a/c. There are a couple ways to make this more rigorous/elegant. The topological approach is to think of ℂ ∪ ∞ as the Riemann sphere. The algebraic approach is to think of it as a projective space.
Now let’s turn to finite fields, say the integers mod 17, which we will write as ℤ17. For a concrete example, let’s set a = 3, b = 8, c = 6, and d = 5. Then ad – bc = 1 mod 17. The multiplicative inverse of 6 mod 17 is 3, so we have a hole in the domain when
z = −d/c = −5/6 = −5 × 3 = − 15 = 2 mod 17.
Following the patch used with complex numbers, we define g(2) to be ∞, and we define
g(∞) = a/c = 3/6 = 3 × 3 = 9 mod 17.
That’s all fine, except now we’re not actually working over ℤ17 but rather ℤ17 ∪ ∞. We could formalize this by saying we’re working in a projective space over ℤ17. For this post let’s just say we’re working over set G with 18 elements that mostly follows the rules of ℤ17 but has a couple additional rules.
Now our function g maps G onto G. No holes.
Here’s how we might implement g in Python.
def g(n):
if n == 2:
return 17
if n == 17:
return 9
a, b, c, d = 3, 8, 6, 5
denom = c*n + d
denom_inverse = pow(denom, -1, 17)
return (a*n + b)*denom_inverse % 17
The plot at the top of the post arranges 18 points uniformly around a circle and connects n to g(n).
from numpy import pi, linspace, sin, cos
import matplotlib.pyplot as plt
θ = 2*pi/18
t = linspace(0, 2*pi)
plt.plot(cos(t), sin(t), 'b-')
for n in range(18):
plt.plot(cos(n*θ), sin(n*θ), 'bo')
plt.plot([cos(n*θ), cos(g(n)*θ)],
[sin(n*θ), sin(g(n)*θ)], 'g-')
plt.gca().set_aspect("equal")
plt.show()
Application to cryptography
What use is this? Möbius transformations over finite fields [1] are “higgledy-piggledy” in the words of George Marsaglia, and so they can be used to create random-like permutations. In particular, Möbius transformations over finite fields are used to design S-boxes for use in symmetric encryption algorithms.
Related posts
[1] Technically, finite fields plus an element at infinity.
[2] “If the [pseudorandom] numbers are not random, they are at least higgledy-piggledy.” — RNG researcher George Marsaglia
The post Möbius transformations over a finite field first appeared on John D. Cook.