The elliptic curves used in cryptography are over finite fields. They’re not “curves” at all in the colloquial sense of the word. But they are defined by analogy with continuous curves, and so most discussions of elliptic curves in cryptography start by showing a plot of a real elliptic curve.
Here’s a plot of y² = x³ + 2 for real x and y.
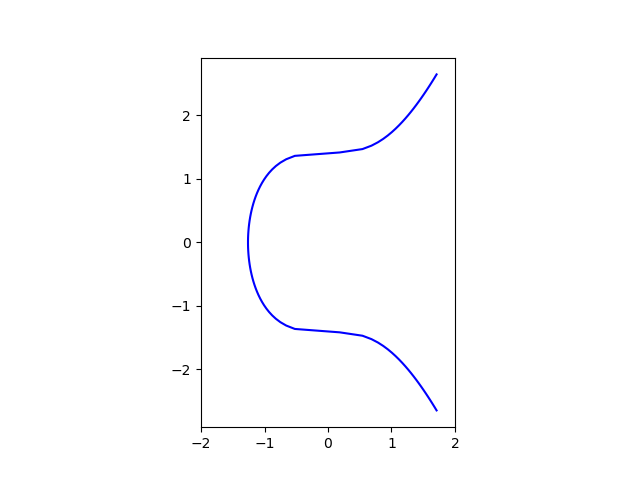
That’s fine as far as it goes. Resources quickly go on to say that the curves they’ll be looking at are discrete, and so they may then add something like the following. Here’s the same elliptic curve as above over the integers mod 11.
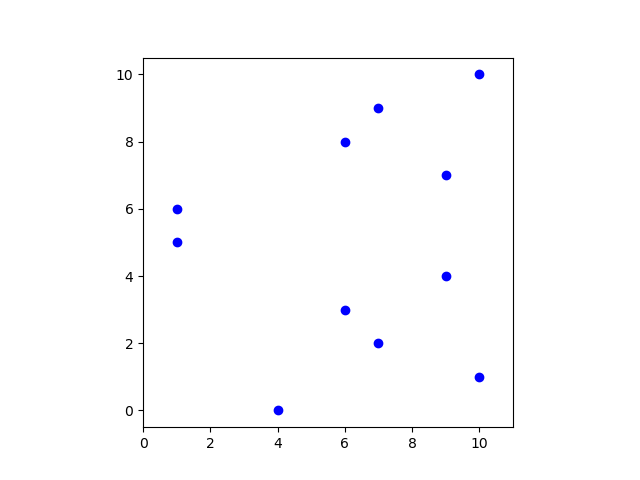
And again mod 997.
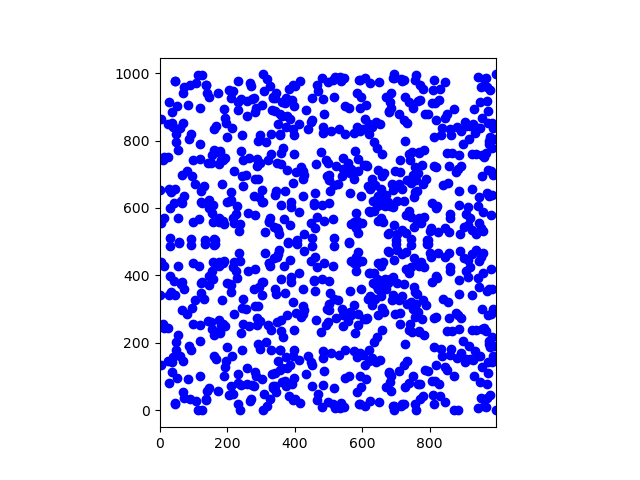
These plots are informative in a couple ways. First, they show that the elements of the curve are discrete points. Second, they show that the points are kinda randomly distributed, which hints at why elliptic curves might be useful in cryptography.
But the implied density of points is entirely wrong. It implies that the density of elliptic curve points increases with the field size increases, when in fact the opposite is true. The source of the confusion is using dots of constant size. A checkerboard graph would be better. Here’s a checkerboard plot for the curve mod 11.
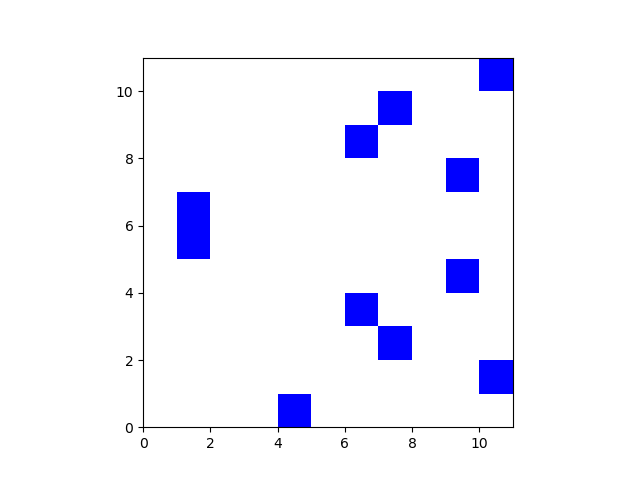
If we were to do the same for the curve mod 997 we’d see nothing. The squares would be too small and too few to see. Here’s a plot for the curve mod 211 that gives a hint of the curve elements as dust in the plot.
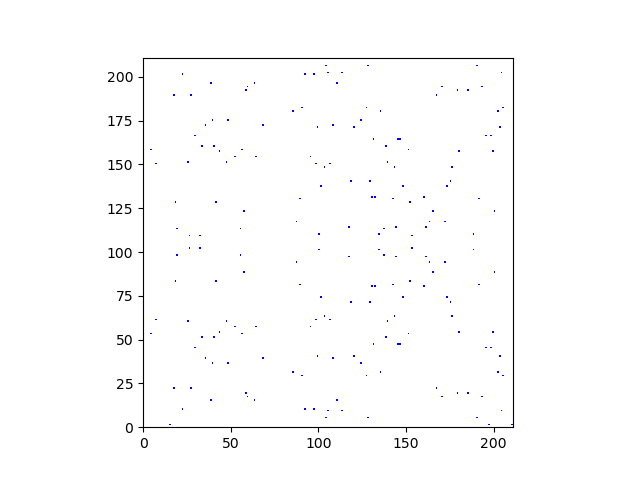
An elliptic curve over the integers modulo a prime p lives in a p by p grid, and the number of points satisfying the equation of an elliptic curve is roughly p. So the density of points in the grid that belong to the curve is 1/p.
The elliptic curves used in cryptography are over fields of size 2255 or larger, and so the probability that a pair of x and y values chosen at random would be on the curve is on the order of 2−255, virtually impossible.
We can be more precise than saying the number of points on the curve is roughly p. If p isn’t too large, we can count the number of points on an elliptic curve. For example, the curve
y² = x³ + 2 mod p
has 12, 199, and 988 points when p = 11, 211, and 997. (If you count the points in the plots above for p = 11 you’ll get 11 points. Elliptic curves always have an extra point at infinity not shown.)
Hasse’s theorem gives upper and lower bounds for the number of points N on an elliptic curve over a field of p elements with p prime:
|N − (p + 1)| ≤ 2 √p.
The heuristic for this is that the right hand side of the equation defining an elliptic curve
x³ + ax + b
is a square mod p above half the time. When it is a square, it corresponds to two values of y and when it is not it corresponds to zero points. So on average an elliptic curve mod p has around p ordinary points and one point at infinity.
Related posts
The post Misleading plots of elliptic curves first appeared on John D. Cook.