The Mandelbrot set is one of the most famous fractals. It consists of the complex numbers c such that iterations of

f(z) = z² + c

are bounded. The plot of the Mandelbrot set is a complicated image—it’s a fractal, after all—and yet there’s a simple description of an first approximation to the Mandelbrot set.

As shown in [1], the image of the disk

A = {α : |α| < ½}

under the map taking z to z − z² gives the set of all points where iterations of f converge to a point.

Also show in [1] is that the points

B = {c : |1 + c| < ¼}

are the ones such that f(f(z)) converges to a fixed point.

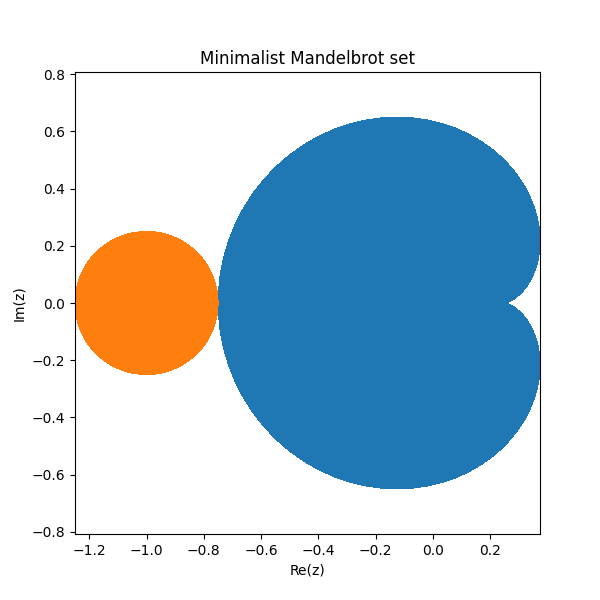
These two parts form the core of the Mandelbrot set. The blue heart-shaped region on the right is A and the orange disk on the left is B.

The rest of the Mandelbrot set are the points where iterations of f remain bounded but have more complicated behavior than the points in A or B.

[1] Alan F. Beardon. Iteration of Rational Functions. Springer-Verlag, 1991.

The post Minimalist Mandelbrot set first appeared on John D. Cook.