Learn how to simulate the flocking behavior observed in birds or fish through simple interaction rules to yield complex crowd dynamics. To this end, we’ll also explore the implementation of a trackball camera and the setup of Dear ImGui with OpenGL and GLFW

Photo by Barth Bailey on Unsplash

1. Boids Theory

Introduction

Craig Reynolds’ “boid” concept, born in the late 1980s, is a pivotal idea in computer graphics and artificial life.

It simulates the collective behavior of birds, fish, and other group-oriented organisms. This algorithm relies on a few fundamental rules governing individual interactions to generate lifelike simulations of group dynamics.

“boid” is the contraction of bird-oid, which means having a bird-like shape, just as “cuboid,” “ellipsoid,” or “deltoid.”

Have a look at Craig Reynolds’ personal website.

Basic interaction rules

Let’s consider animating a flock of N birds. Rather than scripting the detailed behavior of each bird, which would be a laborious task, we can provide them with simple interaction rules and let the magic happen.

Here are the three fundamental rules:

  • Alignment: Align with the average orientation of the local group
    (Main trajectory of the flock)
  • Separation: Avoid being too close to neighbors
    (No conflicts inside the flock)
  • Cohesion: Move toward the average position of the local group
    (Compactness of the flock)

In the screen recording below, I dynamically adjust the weighting of the Alignment to enforce a common trajectory to the flock.

As you might have noticed, I used the boid orientation to define its color. That way, we can easily detect orientation patterns.

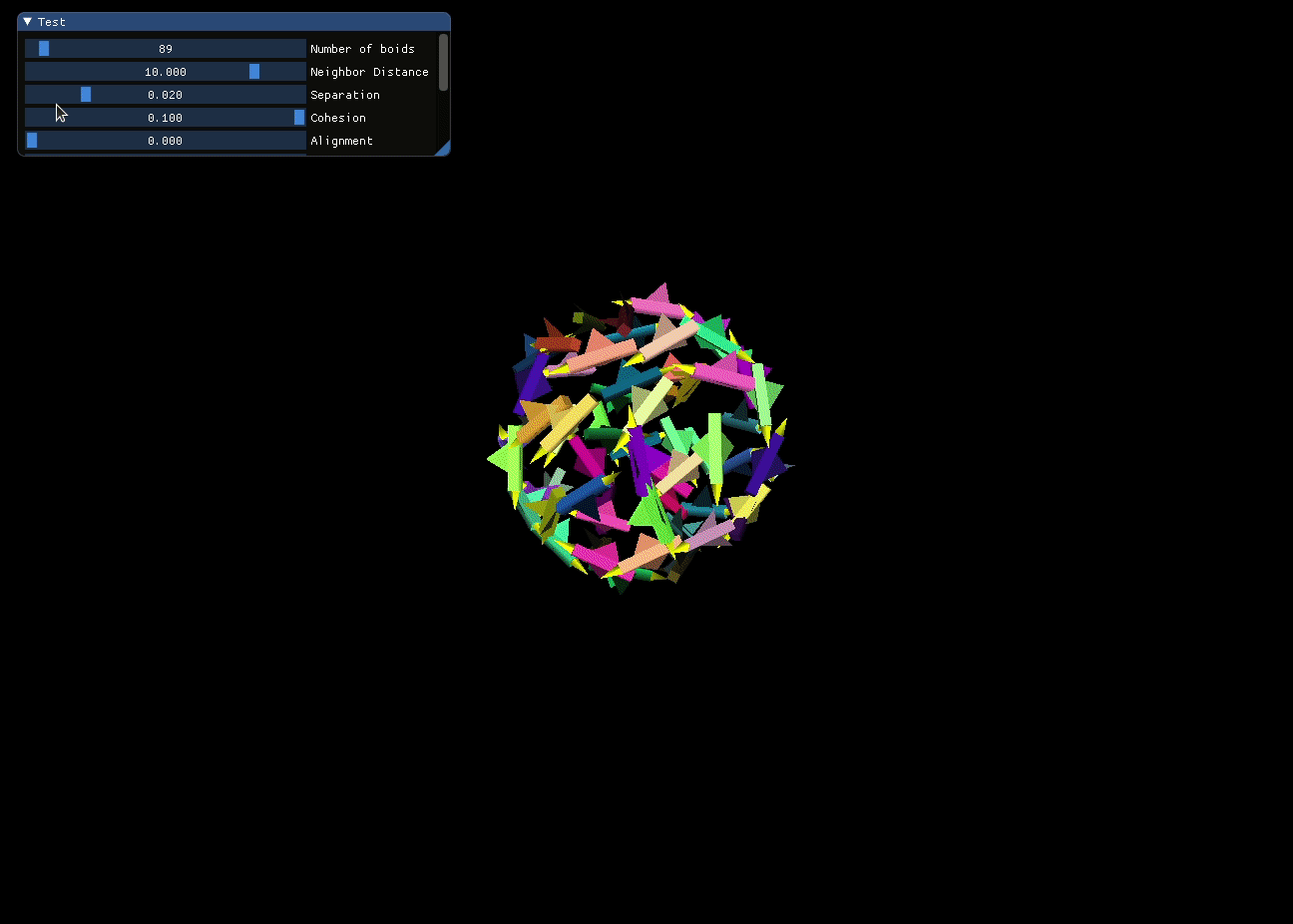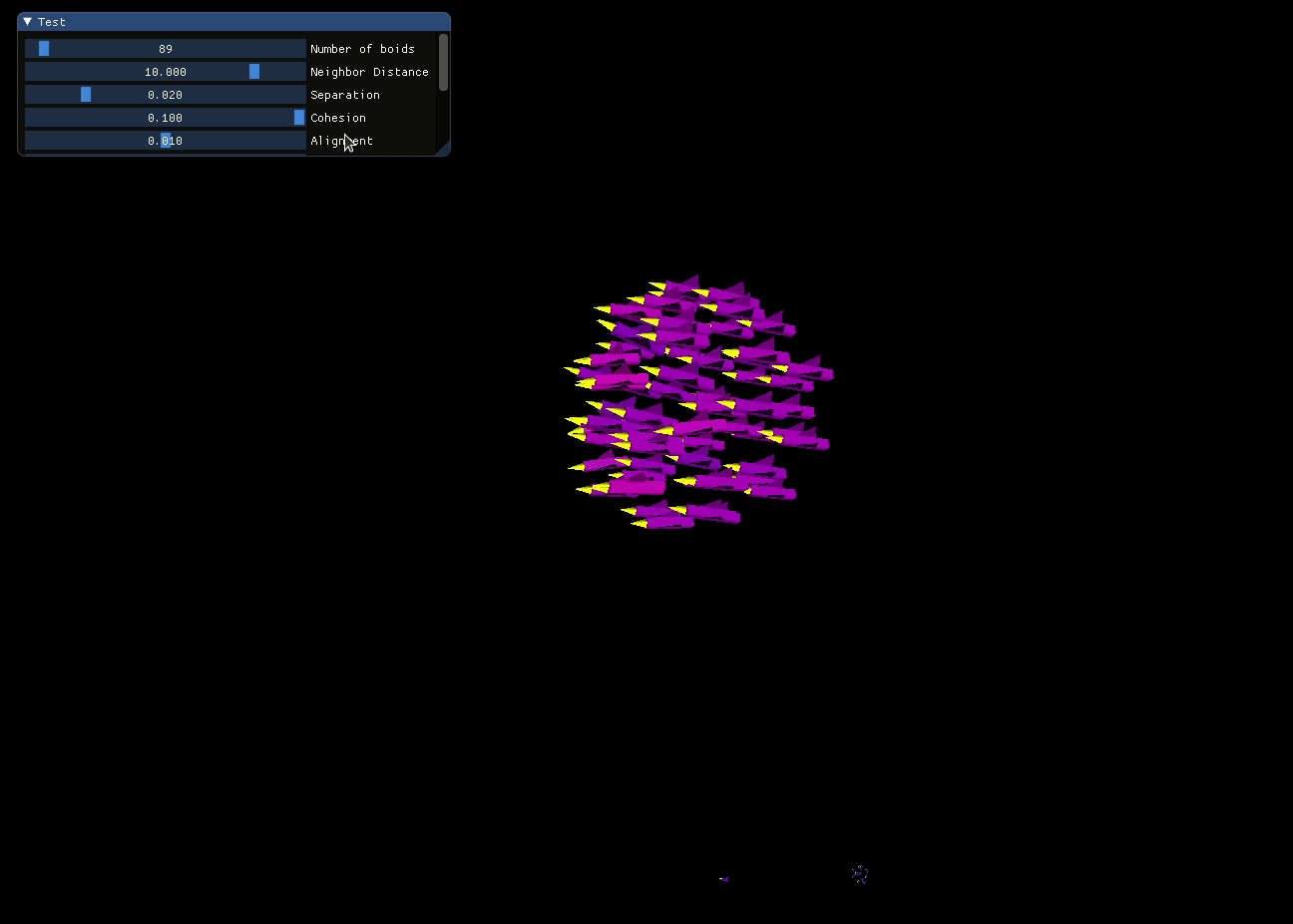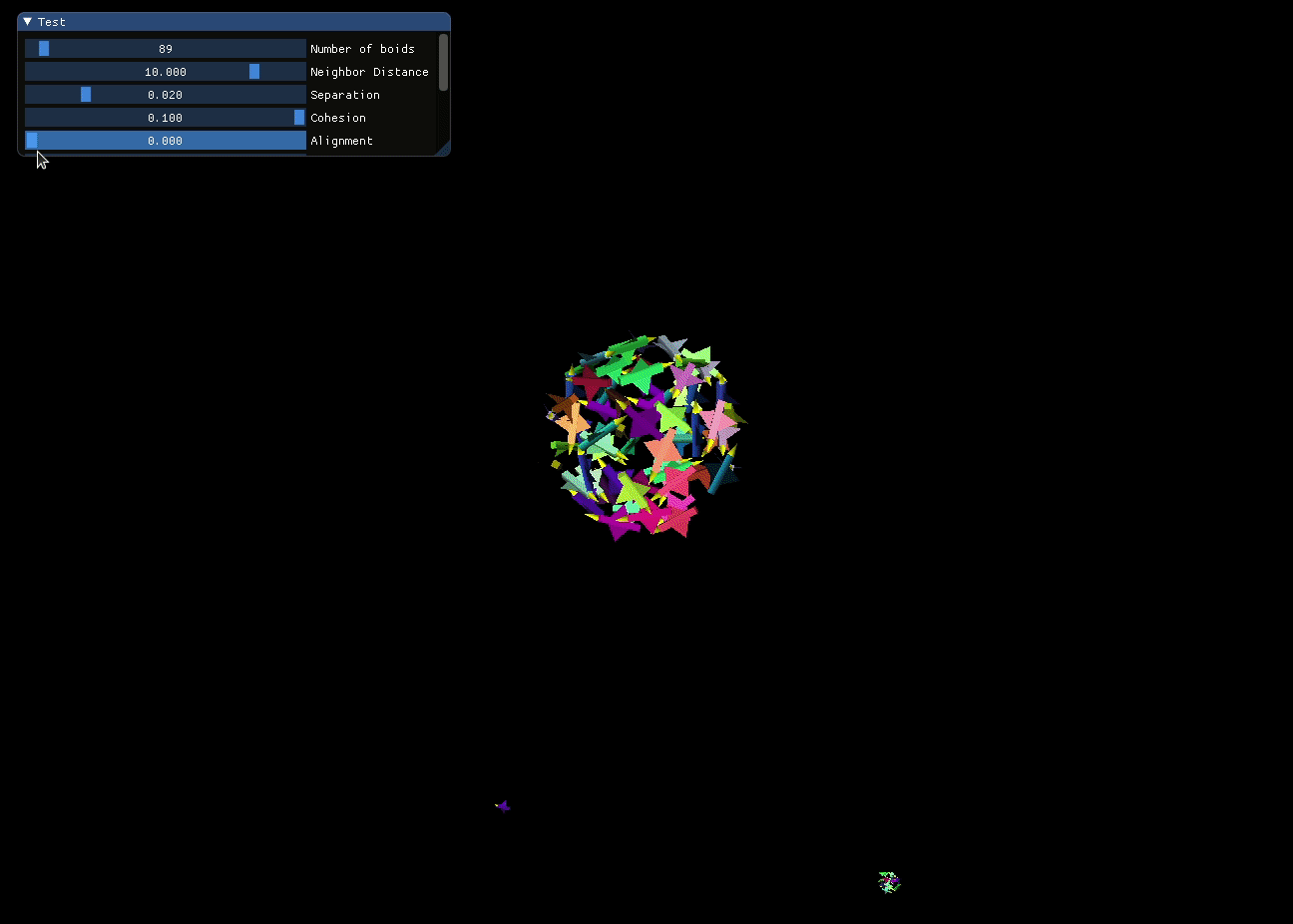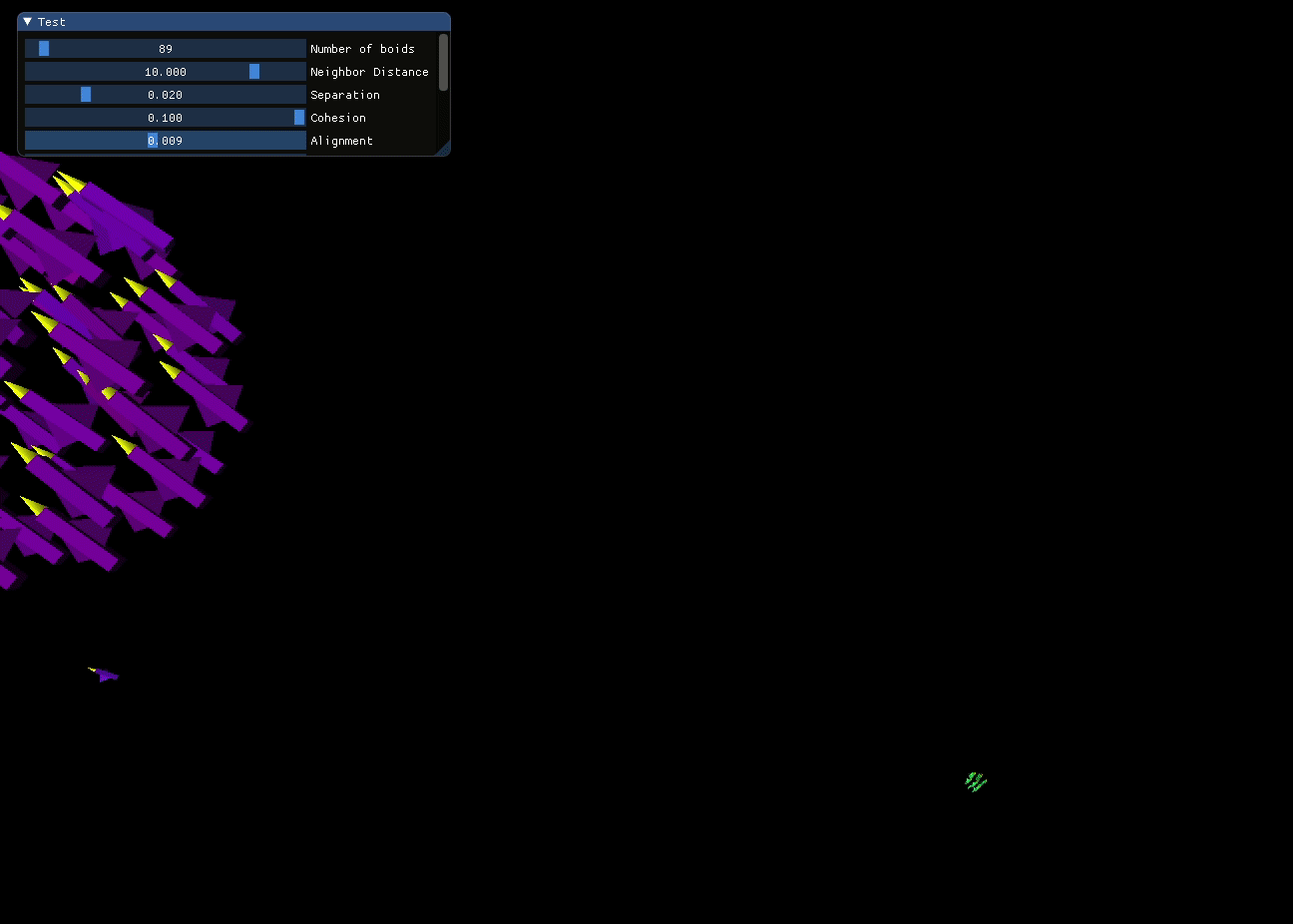
Effect of the Alignment rule — Screen recording by the author

Separation and Cohesion are closely related but operate within distinct distance ranges. Separation only comes into play when a boid enters the individual “comfort zone” of another boid, whereas Cohesion guarantees that all the boids unite as a connected entity.

In the screen recording below, I dynamically adjust the weighting of the Separation and Cohesion rules to observe their real-time effects on the simulated crowd.

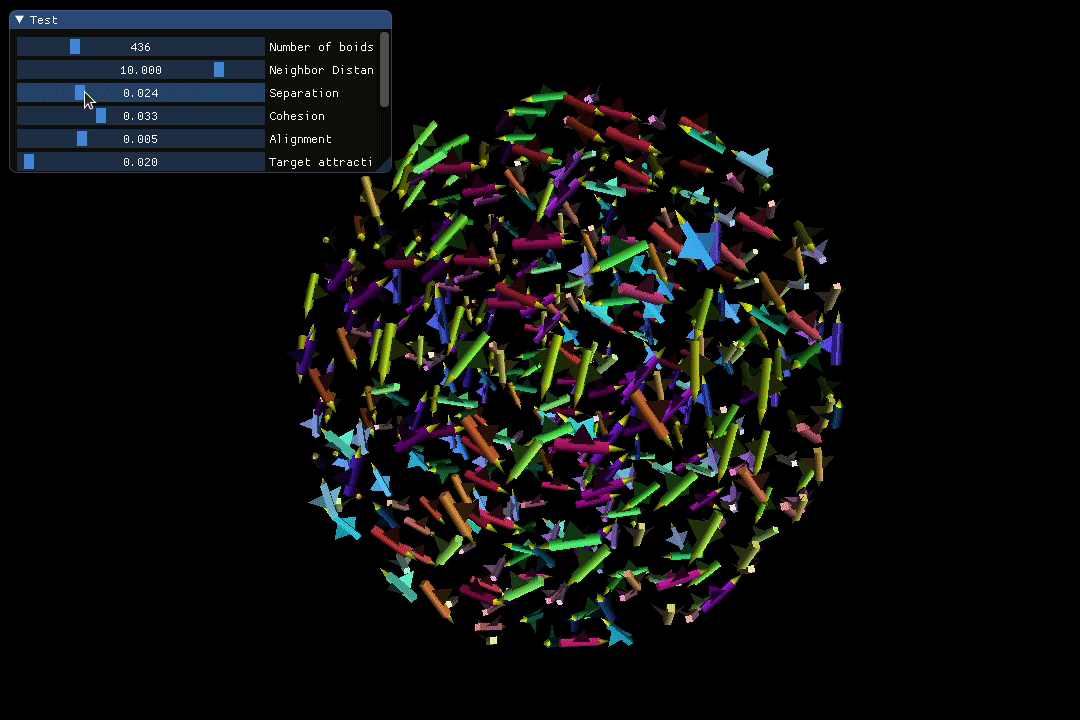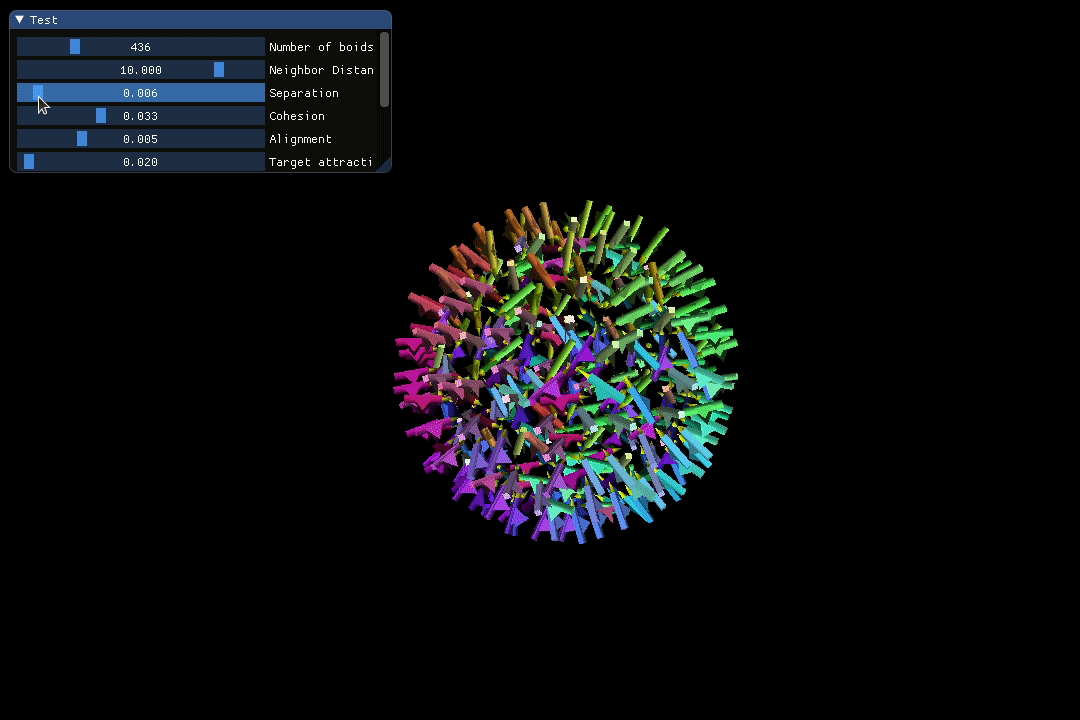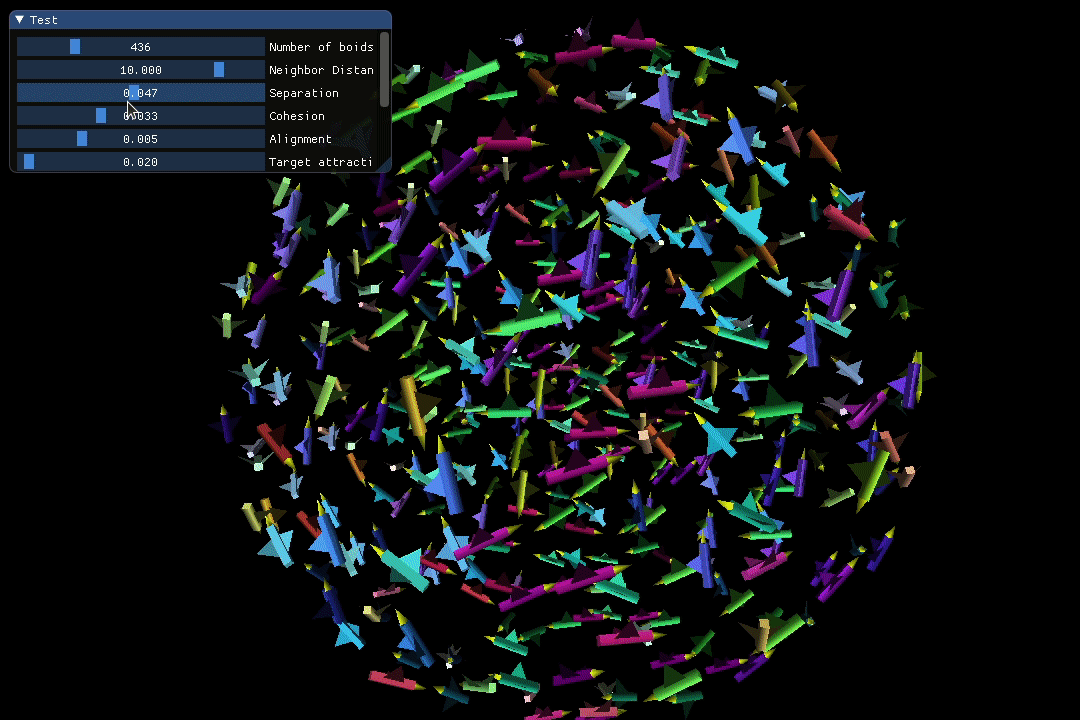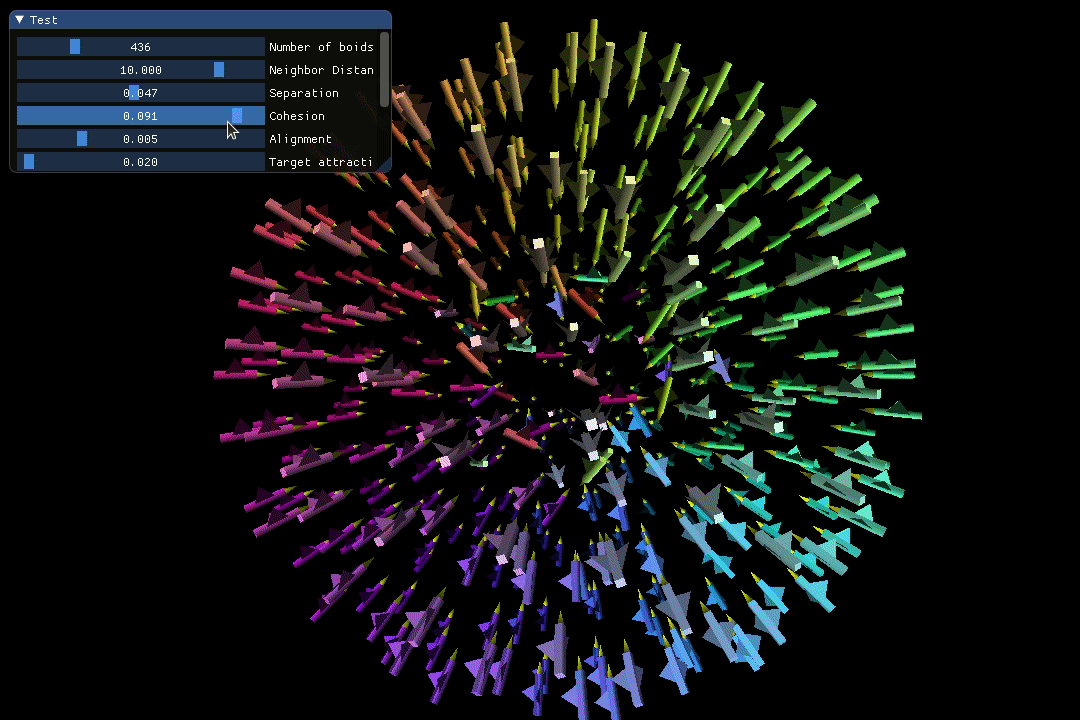
Effect of the Separation/Cohesion rule — Screen recording by the author

The screen recording below showcases a visually appealing loop pattern spontaneously created by the flock during the simulation.

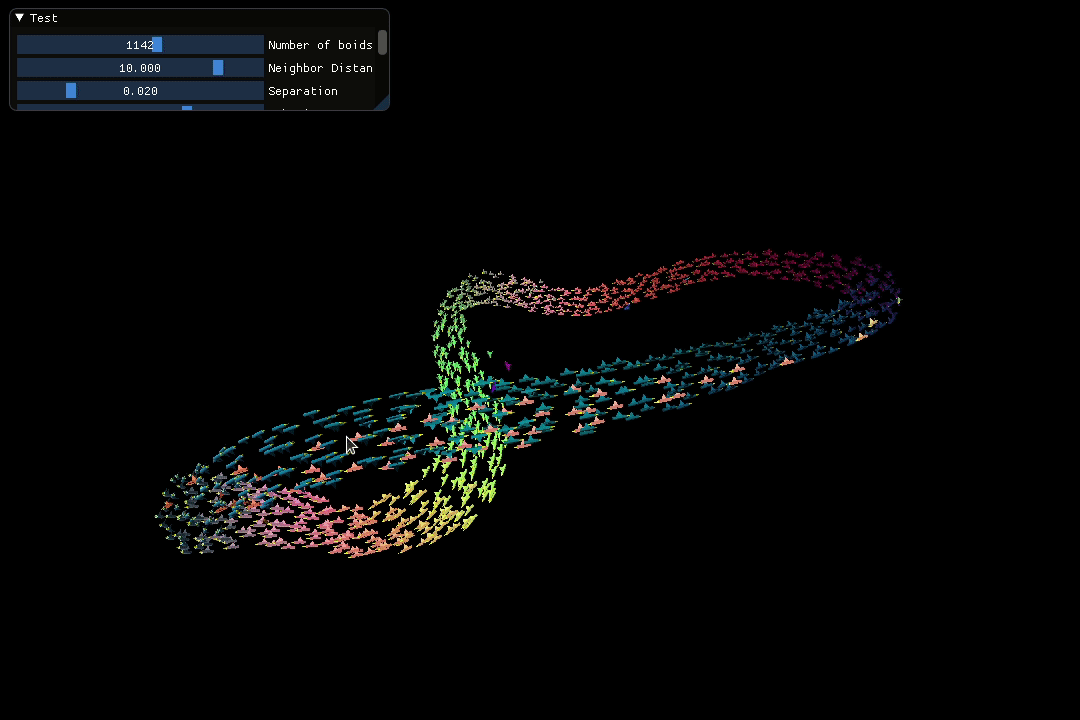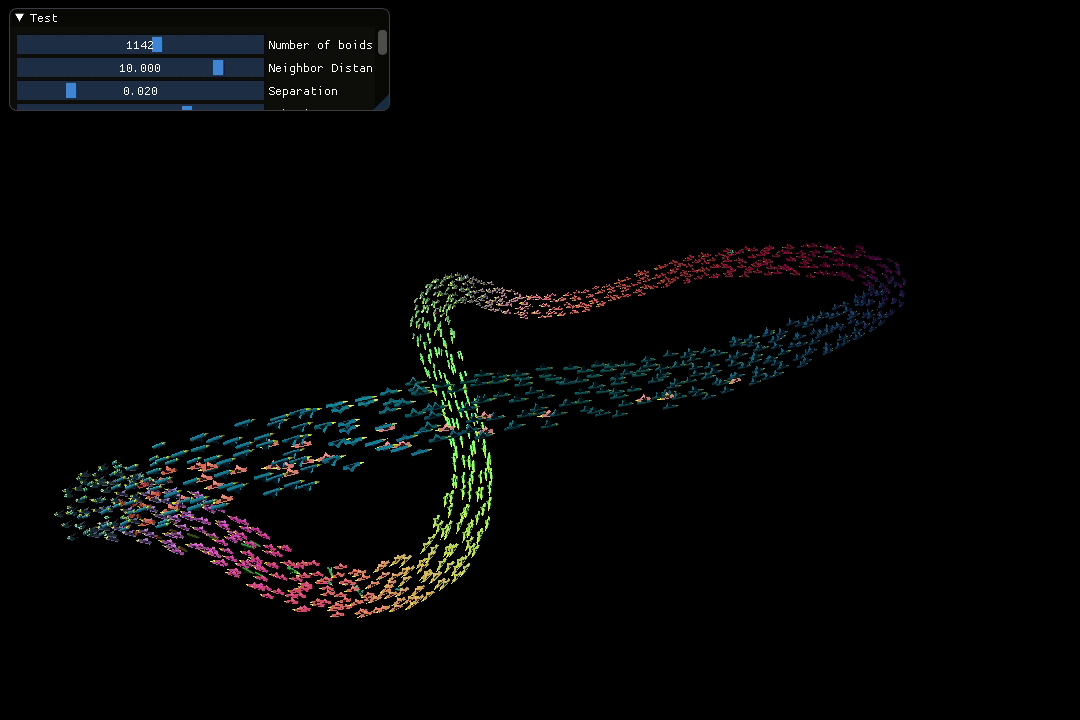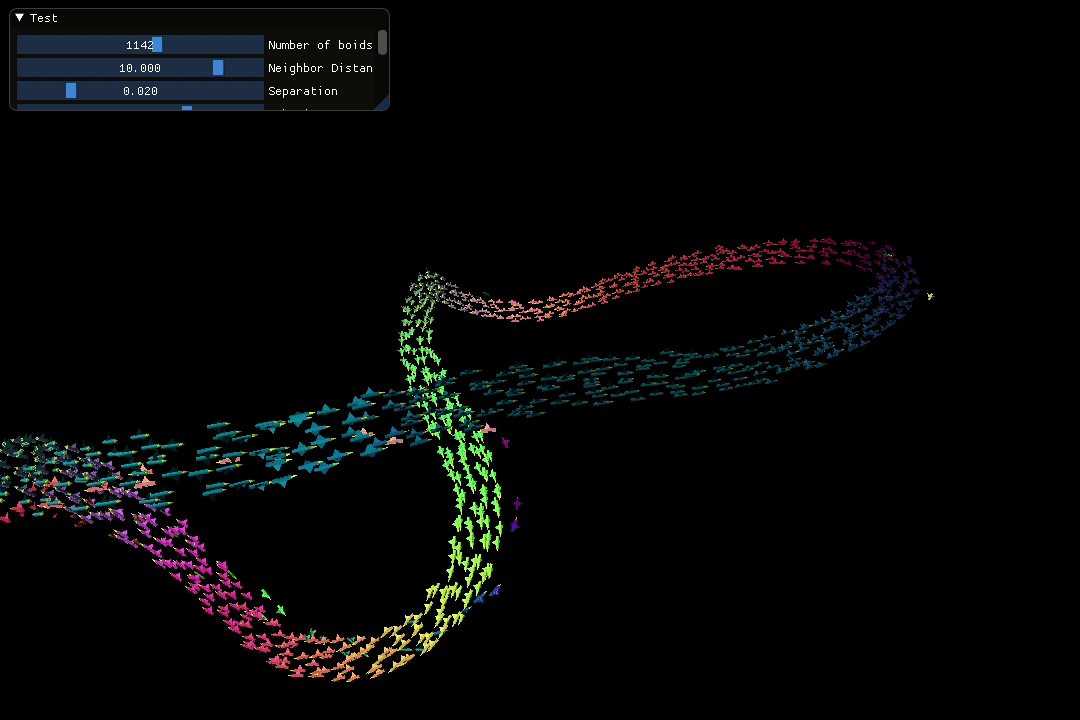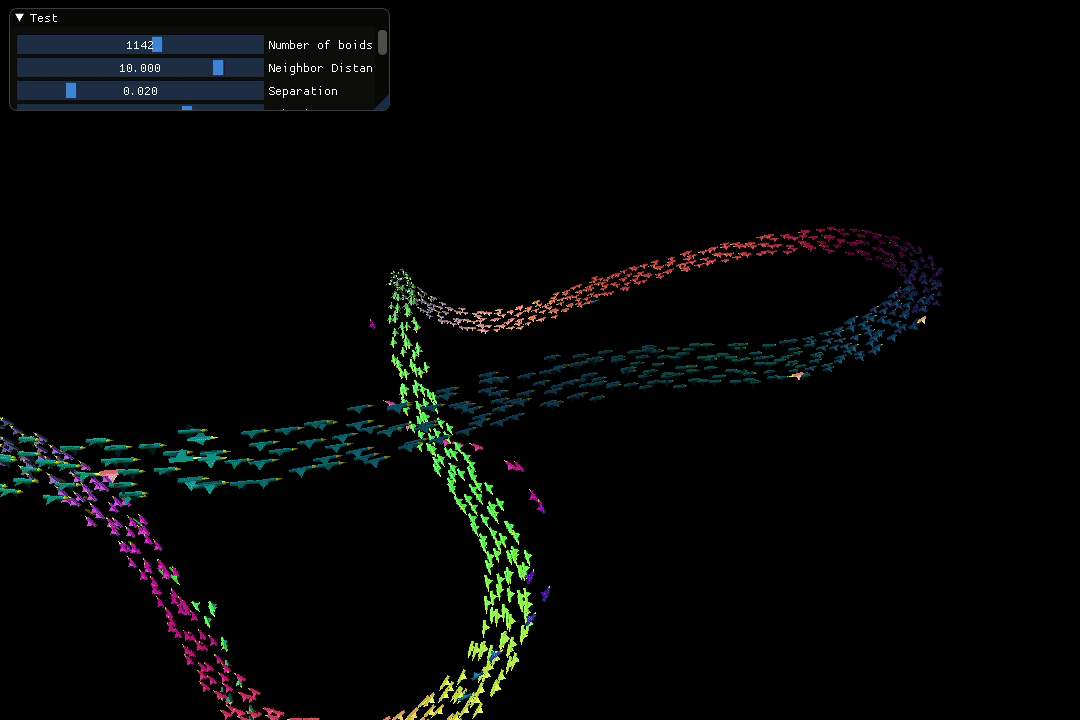
Boids following each other in a loop — Screen recording by the author
Photo by Danil Shostak on Unsplash

2. C++ Implementation

Equations

Newton’s second law of motion defines the connection between the dynamics of boids and the interaction rules/forces that govern them.

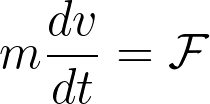
For a boid of index i, we can aggregate the interaction rules in the force presented below. Where Ni refers to the set of indices of the local neighbors of the boid i.

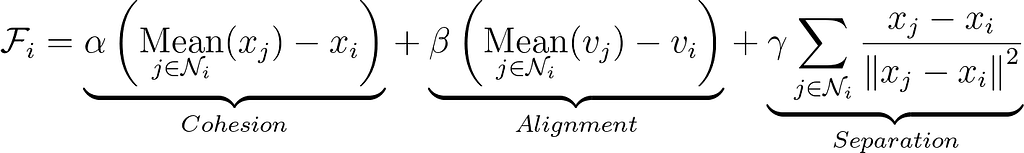
Cohesion and Alignment forces are influenced by the distance to the position or speed of the local group, while the Separation force is determined by the reciprocal distance between two boids.

The α, β, and γ coefficients enable the adjustment of the relative importance of each force.

However, keep in mind that there are plenty of other possible feedback control mechanisms for these three rules.

The update equations below are a direct consequence of the second law, assuming that the boid’s mass remains constant and is embedded within the α, β, and γ coefficients.

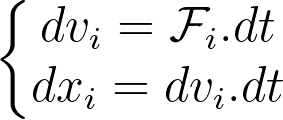
Boids update

We could use Eigen to store our 3D vectors, but since we will be using OpenGL later on, it makes sense to work with GLM immediately. You can install it using apt-get install libglm-dev.

OpenGL Mathematics (GLM) is a header only C++ mathematics library for graphics software based on the OpenGL Shading Language (GLSL) specification.

For the sake of readability, I’ve displayed only the implementation’s core body to avoid burdening the reader with excessive C++ verbosity. Feel free to use either functional or object-oriented programming.

Since the boids’ positions and speeds must be updated simultaneously, we can’t do the update in a single pass. As a first step, the code below merely iterates over all the boids pairs to store the neighbors and precompute the separation forces.

Note: The neighborhood relationship isn’t necessarily reciprocal. We could add a Field Of View parameter so that boids don’t perceive other boids behind their back.

Finally, we sum up the forces and update the boids’ positions and speeds. Beyond a specific speed threshold, the boid’s velocity is capped to ensure stability in the dynamics.

Note: This requires to have access to the elapsed time since the last update.

Bonuses

There are plenty of other forces or mechanisms that can be implemented:

  • Set a maximum angular speed change to avoid “flipping” boids
  • Add moving target objects that attract boids
  • Introduce obstacles such as walls that boids are prevented from crossing.

For instance, in the screen recording below, boids pass through two holes inside a wall to reach an attractive target.

Boids passing through two holes to reach a target — Screen recording from the author
Photo by Shubham Dhage on Unsplash

3. OpenGL Animation

Introduction

OpenGL is a great choice for developing a C++ application to animate boids due to its versatility and high-performance capabilities.

OpenGL (Open Graphics Library) is a cross-platform, open-source graphics API that facilitates GPU-accelerated rendering and enables developers to efficiently create interactive 2D and 3D graphics within their applications.

GLFW, which stands for “Graphics Library FrameWork,” is often used with OpenGL to simplify window creation, user input handling, and context management, making it a popular choice for many OpenGL projects. Alternative libraries like SDL, FreeGLUT, and SFML can also be used depending on the specific requirements of your OpenGL project.

You can install both OpenGL and GLFW using the following command:
apt-get install libgl1-mesa-dev libglfw3-dev

Dear ImGui

Dear ImGui, or “Immediate Mode Graphical User Interface,” is a lightweight and efficient library for creating dynamic user interfaces in real-time applications. It’s especially popular in game development and other projects requiring flexible in-app interfaces.

The screen capture below illustrates how the Dear ImGui interface smoothly blends with the OpenGL application.

Dear ImGui interface — Screen capture by the author

The core of Dear ImGui is self-contained within a few platform-agnostic files which you can easily compile in your application/engine. They are all the files in the root folder of the repository (imgui*.cpp, imgui*.h).

No specific build process is required. You can add the .cpp files into your existing project. Backends for a variety of graphics API and rendering platforms are provided in the backends/folder.

Adding ImGui with opengl3 and glfw backends— Screenshots by the author

Trackball camera

Using Dear ImGui allows users to make real-time parameter adjustments, directly influencing the flock’s behavior on-screen. To optimize the user experience, we should also offer an intuitive mouse-based control mechanism to navigate inside the 3D environment.

A frequently chosen approach is to implement a trackball camera, which allows one to rotate and zoom around a position in space that can be changed dynamically.

This camera is defined by:

  • a 3D point in space that the camera will focus on, i.e., a point that will always be projected in the center of the screen
  • its spherical coordinates around this fixed point, i.e., two angles φ and θ and a radius r used to zoom in/out
Trackball Camera — Diagram by the author

I’ve chosen the RIGHT_DOWN_FRONT camera convention to easily match with the mouse events (You can also experiment with negating the dx and dy values within the mouse events to adjust navigation to your preference.).

If you’re not familiar with camera poses and coordinate systems, have a look at my previous articles: Converting camera poses from OpenCV to OpenGL can be easy and Understanding 360 images 🌎.

Let’s look at the expected camera behavior before actually implementing it. Three colored cubes are being rendered, and a white cross is superimposed to represent the center, i.e., the 3D point that the camera is looking at.

The rotation consists of using the left-click drags to update φ and θ. Horizontal mouse moves update θ, while vertical ones update φ. Although θ covers a range of 2π, while φ only covers π, it makes more sense to treat horizontal and vertical mouse movements with equal influence when adjusting these angles.

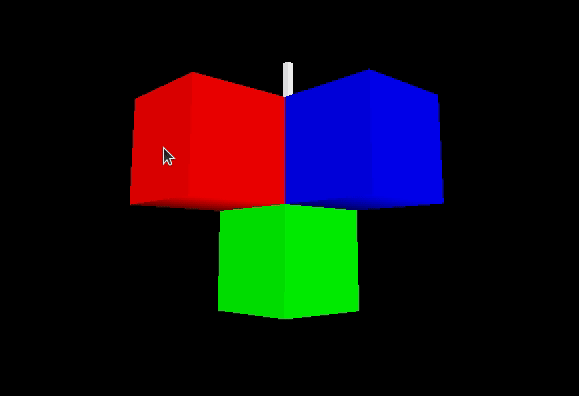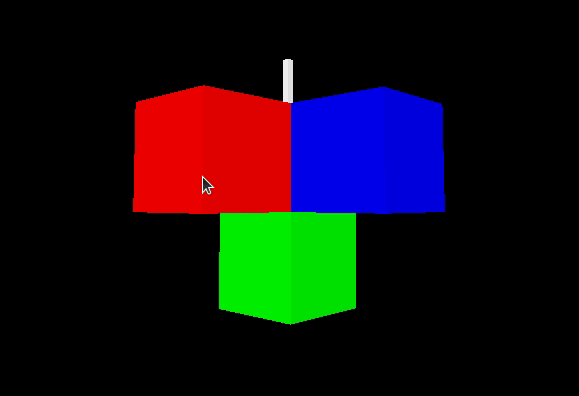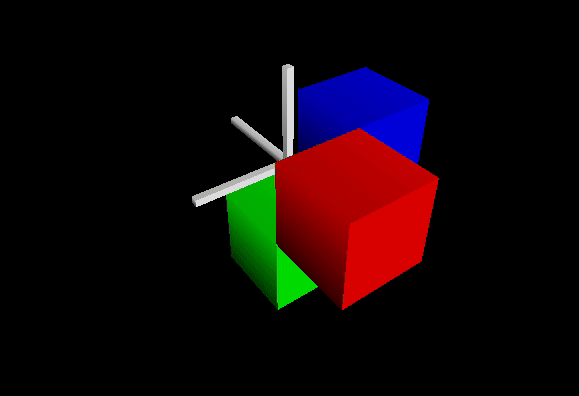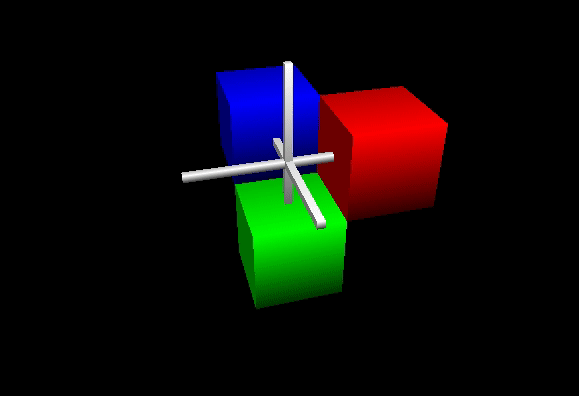
Rotation — Screen Recording by the author

The zoom consists of shrinking or increasing the radius r.

Zoom — Screen Recording by the author

The center shift uses the right-click drag to translate the center position along the fronto-parallel plane.

Center shift — Screen Recording by the author

Here’s the header of the TrackballCamera class.

The compute_axes method returns the current camera’s right, down, and front axes. Note that we need to flip the vector given by the spherical angles φ and θ to obtain the front vector since the camera is looking toward the center.

Since the front vector isn’t necessarily orthogonal to the up vector aligned with the gravity, the cross-product hack is required to obtain an orthonormal basis, with an up vector lying within the vertical plane.

Assuming the mouse drags dx and dy have been scaled inside [-1,1], we can use them to update the camera parameters, as explained previously. The signed zoom_input is the number of mouse scrolls.

Finally, we can define the OpenGL model view matrix by looking at a distance r from the center.

Boid drawing

When rendering objects with OpenGL, it’s often useful to combine basic geometric primitives like vertices, edges, and faces with matrix transformations. This approach allows us to define these primitives within their local coordinate systems, essentially their isolated spaces. We can then apply matrix transformations to these local primitives to translate, rotate, or scale them within the global scene.

It would be incredibly tedious and impractical to define every primitive, such as vertices of a 3D model, in a global coordinate space.

The glPushMatrix/glPopMatrix methods allow you to isolate transformations and avoid cumulative effects by saving a checkpoint for the current matrix state.

Let’s create a simple representation of a boid by rendering a thin colored box as its body and a yellow pyramid to depict its beak.

Boids Drawing — Screen Capture by the author

First, we must apply a transform to align the X-axis with the boids orientation. This can be done by first translating to the boid position and then rotating around the cross product between the X-axis and the speed vector. Note that to compute the angle θ between two vectors, which is inside [0, π], it’s more robust to use atan2 than directly the acos method.

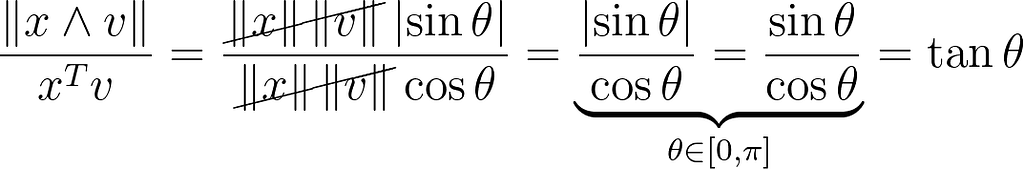
The draw_box and draw_pyramid methods define the vertices to link together.

Final OpenGL Script

Here’s the final script to run the OpenGL app using GLFW, Dear Imgui, and our custom Trackball Camera. For the sake of readability, the mouse callbacks are defined in a second snippet.

There’s a placeholder TODO line in the rendering loop to add the boids update and rendering.

We create a GLFW context, followed by a Dear Imgui context. Then, as long as the window is open, new frames are created and rendered at 30 FPS.

While the Model View matrix is updated by the lookAt method of the TrackballCamera, the Projection matrix is constantly adjusted to match the current window size.

Dear ImGui allows us to update a float and an integer using sliders.

Here are the mouse callbacks, calling the zoom , rotate and shift_center methods of the TrackballCamera.

Conclusion

I hope you enjoyed reading this article and that it gives you more insights on how to animate boids using Dear ImGui!

Click here to go to my GitHub repository.

Mastering Flock Simulation with Boids, C++, OpenGL and ImGui 🐦 was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.

Previous Post
Next Post