The two latest posts have been about the Mandelbrot set, the set of complex numbers c such that iterations of
f(z) = z² + c
remain bounded. It’s easy to see that the sequence of iterates will go off to infinity if at any step |z| > 2.
For each c, we can look at the escape time, the number of iterations it takes before an value has magnitude greater than 2. The Mandelbrot set is the set of points with infinite escape time.
In the plot below, I sampled 1,000,000 points at random and colored each according to the corresponding escape time. The lighter blue color corresponds to earlier escape.
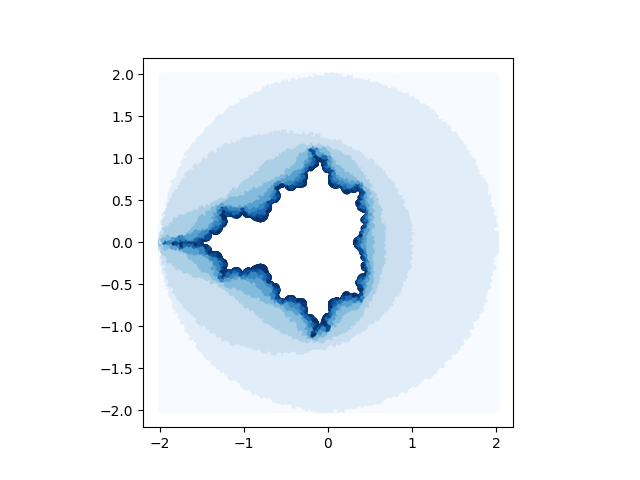
The white points in the interior have an escape time of more than 10 (and possibly infinity).
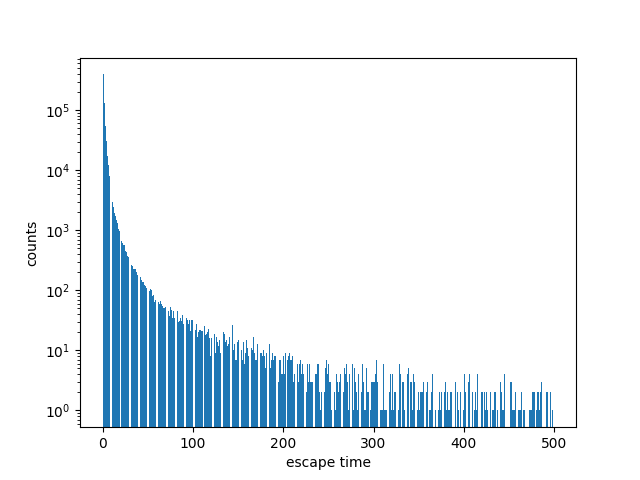
When plotting the Mandelbrot set, how do you know whether a point will never escape? You don’t, not with certainty. But by looking at the distribution of escape times you can see that most points that are going to escape do so quickly. For example, after sampling 1,000,000 points, doing 2000 iterations for each point, 99.9% of points that escape do so within 248 iterations.
If we were to plot a histogram of the escape times it would simply look like a spike on the left end. Using a logarithmic scale for the vertical axis lets us see more of what’s going on. Note that the escape times decrease rapidly, even on a log scale.
By counting what portion of points do not escape, we can calculate a Monte Carlo estimate of the area of the Mandelbrot set, and in fact this is the best way to calculate the area. There is an exact expression for the area in terms of an infinite sum, but the sum converges so slowly that it is unusable; Monte Carlo sampling is faster.
Using 1,000,000 random values of c, a total of 905,444 points from the square [−2, 2] × [−2, 2] escape within 2,000 iterations. Since the square has area 16, this gives us an estimate
A = 16 × (1000000 − 905,444)/1000000 = 1.5129.
A 95% confidence interval for the area is
A ± 16 × 1.96 × (p (1 − p)/1000000) = (1.5082, 1.5176)
where p = 905444/1000000.
A study [1] found the area to be 1.506484 ± 0.000004, which is just outside of our confidence interval. Some of the difference is due to chance, and some of it is due to our stopping at 2000 iterations. If we had gone done more iterations, more points would escape (though not very many, for reasons explained above).
[1] See OEIS A098403
The post Mandelbrot area and escape times first appeared on John D. Cook.