Suppose you’re in a boring meeting and you start doodling. You draw a circle, and then you draw a triangle on the outside of that circle.
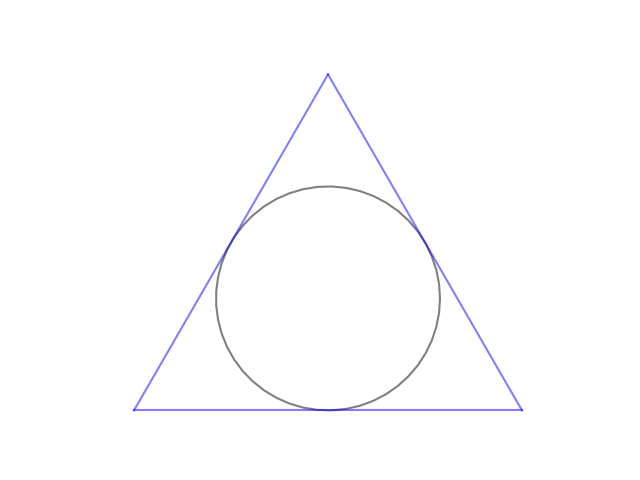
Next you draw a circle through the vertices of the triangle, and draw a square outside that.

Then you draw a circle through the vertices of the square, and draw a pentagon outside that.

Then you think “Will this ever stop?!”, meaning the meeting, but you could ask a similar question about your doodling: does your sequence of doodles converge to a circle of finite radius, or do they grow without bound?
An n-gon circumscribed on the outside of a circle of radius r is inscribed in a circle of radius
So if you start with a unit circle, the radius of the circle through the vertices of the N-gon is
and the limit as N → ∞ exists. The limit is known as the polygon circumscribing constant, and it equals 8.7000366252….
We can visualize the limit by making a plot with large N. The plot is less cluttered if we leave out the circles and just show the polygons. N = 30 in the plot below.

The reciprocal of the polygon circumscribing constant is known as the Kepler-Bouwkamp constant. The Kepler-Bouwkamp constant is the limiting radius if you were to reverse the process above, inscribing polygons at each step rather than circumscribing them. It would make sense to call the Kepler-Bouwkamp constant the polygon inscribing constant, but for historical reasons it is named after Johannes Kepler and Christoffel Bouwkamp.
The post Limit of a doodle first appeared on John D. Cook.