A practical guide to attitude determination with Kalman filtering

Attitude determination, the process of determining the orientation of an object with respect to a fixed reference frame, is an essential aspect of navigation, control, and guidance systems in various fields, such as aerospace, robotics, and autonomous vehicles. Sensor data from these systems are noisy. This is where the Kalman filter, a mathematical algorithm that combines measurements and predictions to estimate the state of a dynamic system, comes in. Kalman filtering is one of the most popular methods for cleaning up noisy sensor data and I am going to show you how you can build your own.
In this article, we will explore how to build an Arduino-based Kalman filter for attitude determination. Building this for an Arduino means it will be a cost-effective and versatile solution for small-scale applications like hobby drones.
We will cover a bit about the theory behind the Kalman filter, the hardware and software requirements, and the implementation of the filter using an Arduino Nano and six-axis (accelerometer + gyroscope) MPU-6050 motion sensor. By the end of this article, you will have a basic understanding of how Kalman filters work and how you can use a Kalman filter for attitude estimation.
What is a Kalman filter?
A Kalman filter is a mathematical algorithm that can be used to estimate the state of a dynamic system from a series of noisy measurements. The Kalman filter was developed by Rudolf E. Kálmán and first described in his seminal paper, published in 1960, “A New Approach to Linear Filtering and Prediction Problems”. The filter is sometimes called the Kalman–Bucy filter owing to contributions to its development by Richard S. Bucy.
Kalman filtering is widely used in a variety of applications that involve estimating or predicting the state of a dynamic system based on noisy measurements. It was in aerospace where Kalman filters were first extensively used in applications such as guidance, navigation, and control of spacecraft, aircraft, and missiles.
One of the most notable use cases was in the Apollo Guidance Computer where they were used for spacecraft state estimation during the Apollo program.

Kalman filtering also finds utility in signal processing and robotics applications. In signal processing, they have been used for speech enhancement by estimating the underlying signal from noisy measurements and removing noise from the signal. In robotics applications, they are used to estimate the position and orientation of robots based on sensor measurements from cameras, lidars, and inertial measurement units. Consumer devices such as smartphones, wearables, and gaming controllers employ Kalman filtering to aid with position and orientation estimation.
So, Kalman filters are used in lots of different applications but how does the algorithm work? I don’t go deep into the theory behind Kalman filters in this article. Instead, this article is intended to be a practical guide to implementing a Kalman filter, presented in a form which is easy to understand and follow. The literature on Kalman filters can be frustratingly complex and it doesn’t need to be this way! The algorithm is simple and consists of two main steps:
Prediction step:
Based on the current state of the system and a state space model of that system, the Kalman filter predicts the future state of the system. The state space model is a mathematical representation of how the system evolves over time, and it includes information about the system’s dynamics and any external inputs.
Update step:
The Kalman filter takes new sensor measurements and combines them with the predicted state to update the “best estimate” of the true state of the system. The update step involves calculating the Kalman gain, which is a weighting factor that balances the contributions of the predicted state and the measurement to obtain the most accurate estimate of the true state. The Kalman gain is based on the covariance of the predicted state and the covariance of the measurement error.
The Kalman filter repeats these steps continuously, updating the measured state and the “best estimate” of the true state of the system at each time step.
By combining the predicted state with the measurement in an optimal way, the Kalman filter can provide a more accurate and reliable estimate of the state of the system than would be possible using only the measurements or the predicted state.
Implementation
Hardware

My goal is for the Kalman filter implemented in this article to eventually form part of a quadcopter flight controller. Maintaining a small form factor is therefore important. I also want to keep the cost down in case it turns out I am not a great quadcopter pilot and I find I need to replace the flight controller following unscheduled “landings”. With these considerations in mind, for the filter hardware, we will use the Arduino Nano and MPU-6050. The total cost of the components is about $20 and they are small enough to fit in the palm of your hand.
The Arduino Nano is a compact and versatile microcontroller board based on the ATmega328P microcontroller. The MPU-6050 is a small, low-power, 6-axis motion-tracking device designed for a wide range of applications. It combines a 3-axis gyroscope and a 3-axis accelerometer in a single package, allowing it to accurately measure motion in six degrees of freedom.
The MPU-6050 communicates with the Arduino Nano through the I2C bus. To connect to the I2C bus we connect the SDA and SCL pins on the MPU-6050 to pins A4 and A5 on the Arduino Nano. The MPU-6050 is powered by connecting the VCC pin to the 5V pin on the Arduino Nano and connecting GND to GND. We will power the Arduino Nano by connecting it to a computer. For any applications in the field (i.e. if we want to fly this filter) it can alternatively be battery-powered.

State space model
A state space model is a mathematical representation of a system that changes over time. It is a framework for modeling and analyzing complex systems. We need to construct a state space model which, given our knowledge about the current state of the system, allows us to predict the future state of the system. We will use the state space model in the prediction step of our Kalman filter.
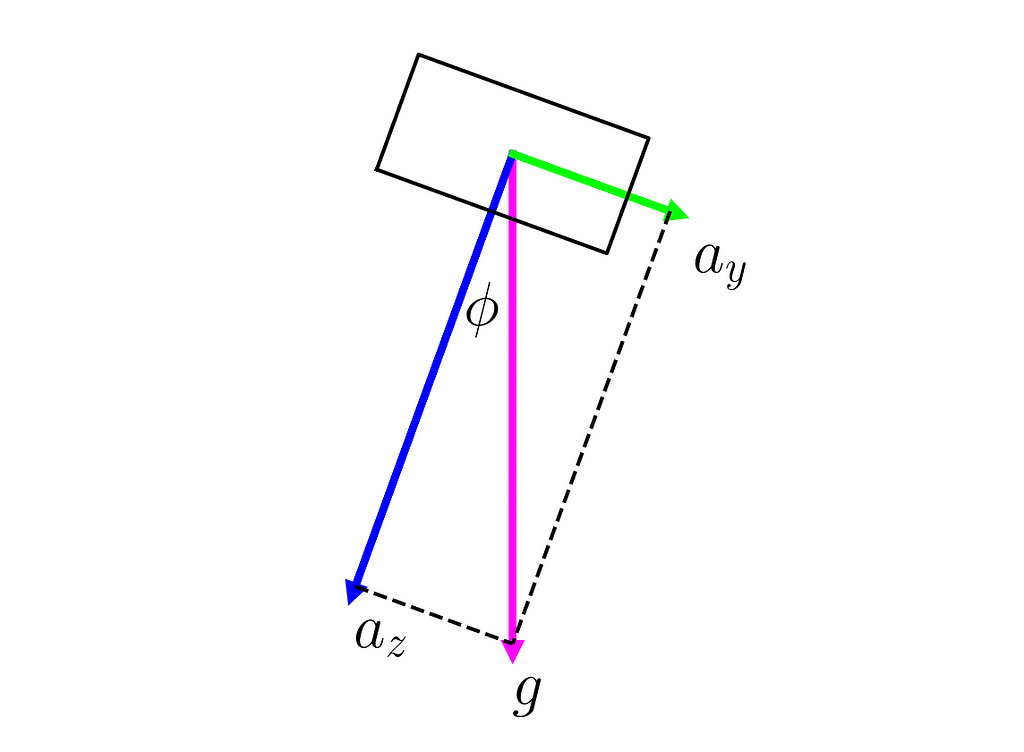
We will track roll and pitch in our Kalman filter. We could extend the filter to include yaw if we connected a magnetometer to the Arduino Nano but in the interest of keeping things simple let’s stick with only working with data from the MPU6050. We can calculate roll and pitch from accelerometer data and we get roll and pitch rates from gyroscope data.
The state space model for our system looks like this:
Where F is the state transition matrix, x is the state vector at time n and n+1 B is the control matrix and u is the control vector at time n. B and u come from known inputs to the system, for example when you are controlling a vehicle you might have information about the forces experienced by your system for a given control input. In our example, B and u are always going to be zero but I include them in the Kalman filter implementation for completeness. F and x are given by:
Where ϕ and θ are the roll and pitch angles and dt is the timestep between each iteration. If we concentrate on the roll angle, all this state-space model says is that the future roll angle is equal to the current roll angle plus the current roll rate multiplied by the timestep. By doing this simple calculation we can predict the future state of our system! Now let’s look at how this, and all the other parts of the Kalman filter, can be implemented programmatically.
Software
In this section, I am going to describe the main parts of the algorithm step by step. If you want to see the full source code for the PlatformIO project, you can download it from this GitHub repository.
For implementing a Kalman filter it is advantageous to be able to write code in such a way that it resembles matrix notation. Fortunately, many libraries exist which allow us to do just this. I chose BasicLinearAlgebra for this purpose. BasicLinearAlgebra is a lightweight library for Arduino which provides a Matrix class for declaring 2D matrices and overrides for basic operators like +, +=, -, -=, *, *= and = so we can use them in algebraic expressions. The ~ operator preceding a Matrix in BasicLinearAlgebra denotes the transpose of that Matrix.
With the BasicLinearAlgebra library, we can declare variables like F and x from our state space model as follows:
BLA::Matrix<4, 1> x = {0.0, 0.0, 0.0, 0.0}; // State [roll, pitch, roll_rate, pitch_rate]
const BLA::Matrix<4, 4> F = {1.0, 0.0, dt, 0.0,
0.0, 1.0, 0.0, dt,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0}; // State transition matrix
The first step in the Kalman filter algorithm is the prediction step. We do this inside the get_prediction() method:
void get_prediction()
{
x = (F * x) + (B * u);
P = (F * (P * (~F))) + Q;
}
The calculation for x should be familiar — it is the state space representation of our system and gives us a prediction of the future state of the system. The second equation is the covariance extrapolation equation where P is the covariance matrix of the current and next state of the system and Q is the process noise matrix. Q represents the uncertainty between actual system behavior and the idealized model used by the filter. We will see later how the value used for the process noise matrix impacts the performance of the filter.
We now have a predicted state and a predicted state covariance matrix. If the concept of a covariance matrix sounds a bit complicated, it isn’t — think of it as a measure of how confident we are in our prediction.
Next, we get a new state measurement. We do this by getting raw data from the MPU-6050 and converting it into roll, pitch, roll rate, and pitch rate. This is all done inside a call to a method called get_new_sensor_readings():
void readMPUdata()
{
// Read raw gyroscope and accelerometer data
Wire.beginTransmission(mpu_address); // Start communicating with the MPU-6050
Wire.write(0x3B); // Send the requested starting register
Wire.endTransmission(); // End the transmission
Wire.requestFrom(mpu_address, 14, true); // Request 14 bytes from the MPU-6050
AccX = Wire.read() << 8 | Wire.read();
AccY = Wire.read() << 8 | Wire.read();
AccZ = Wire.read() << 8 | Wire.read();
temperature = Wire.read() << 8 | Wire.read();
GyroX = Wire.read() << 8 | Wire.read();
GyroY = Wire.read() << 8 | Wire.read();
GyroZ = Wire.read() << 8 | Wire.read();
}
void get_z()
{
total_vector_acc = sqrt((AccX * AccX) + (AccY * AccY) + (AccZ * AccZ)); // Calculate the total accelerometer vector
if(abs(AccY) < total_vector_acc) // Prevent asin function producing a NaN
{
z.storage(0, 0) = asin((float)AccY/total_vector_acc) * rad2deg; // roll
}
if(abs(AccX) < total_vector_acc) // Prevent asin function producing a NaN
{
z.storage(0, 1) = asin((float)AccX/total_vector_acc) * -rad2deg; // pitch
}
z.storage(0, 2) = (GyroX / gyro_scale_factor) - roll_rate_offset; // roll rate
z.storage(0, 3) = (GyroY / gyro_scale_factor) - pitch_rate_offset; // pitch rate
}
void get_new_sensor_readings()
{
readMPUdata();
get_z();
}
The roll and pitch angles are determined based on the angle of the gravity vector relative to the sensor and roll and pitch rates is directly from gyroscope measurements. A gyro_scale_factor is applied to transform from sensor units to degrees per second.
Before we can perform the update step we must first calculate the Kalman gain. Kalman gain represents the weight given to the measurements and the predicted state during the update step. This is done in the get_kalman_gain() method:
void get_kalman_gain()
{
inv = BLA::Inverse((H * (P * (~H))) + R);
K = ((P * (~H)) * inv);
}
There are a couple of new matrices that we have not encountered yet so I will quickly describe the here. We have the observation matrix H and measurement covariance matrix R. H transforms between sensor units to engineering units — since we already do this in the get_z() method H resembles the identity matrix I. Note that H resembling I will not always be the case as it depends on the specific implementation of a given Kalman filter, the sensors used, etc. R represents the uncertainty in measurement values. Its value informs the filter of how confident we are in a measurement and therefore can significantly impact filter performance.
We now have everything we need to perform our update step! We do this in the get_update() method:
void get_update()
{
x = x + (K * (z - (H * x)));
P = (((I - (K * H)) * P) * (~(I - (K * H)))) + ((K * R) * (~K));
}
The update step consists of two equations. The state update equation and the covariance update equation. The state update equation calculates the updated state estimate based on the predicted state estimate and the measurements obtained from sensors. The covariance update equation calculates the updated covariance matrix that represents the uncertainty or error in the estimated state of the system.
There is one more step involved in the Kalman filter that I have implemented. That is the continuous adjustment step. This is a type of adaptive filtering technique. We introduce this step since the object that we want to track might not always behave according to the state space model (due to untracked forces acting on the object) and as a result, the state estimate has a large error compared to the true state.
To solve this problem, we will continuously scale the process noise matrix Q based on the normalized state residual epsilon. If epsilon is greater than some predetermined epsilon_max, we can say that the object is manoeuvring so we increase Q. The filter then has less confidence in the idealised state-space model representation of the system and instead tracks the measurement values more closely. Conversely, we then want to scale down the value of Q once epsilon is below epsilon_max. All of this is achieved quite neatly in the scale_Q() method:
void get_residual()
{
y = z - x;
}
void get_epsilon()
{
epsilon = (~y * (inv * y));
}
void scale_Q()
{
if (epsilon.storage(0, 0) > epsilon_max)
{
Q *= Q_scale_factor;
count += 1;
}
else if (epsilon.storage(0, 0) < epsilon_max && count > 0)
{
Q /= Q_scale_factor;
count -= 1;
}
}
That’s it for the software implementation! We now loop through the prediction, update, and continuous adjustment steps to get the next best estimate for the state of our system. There is one more thing we need to consider; tuning the filter.
Tuning the filter
What do we mean when we “tune” a Kalman filter? Remember, the goal of a Kalman filter is to filter noisy sensor data and output a clean signal that accurately tracks the true state of a system. When we tune a Kalman filter what we are doing is iteratively adjusting its parameters to optimise the performance of the filter for a specific system or application. We are mainly concerned with adjusting the process noise matrix Q and measurement covariance matrix R to get the desired filter performance. We also need to select appropriate values for Q_scale_factor and epsilon_max for controlling the continuous adjustment step. Selecting appropriate values for these parameters makes all the difference between “good” and “bad” filter performance.
For the filter we will use a constant acceleration model for defining the process noise matrix Q. At this point we also assume that the process noise is independent between state variables. This results in a diagonal process noise matrix:
BLA::Matrix<4, 4> Q = {pow(dt, 4) / 4, 0.0, 0.0, 0.0,
0.0, pow(dt, 4) / 4, 0.0, 0.0,
0.0, 0.0, pow(dt, 2), 0.0,
0.0, 0.0, 0.0, pow(dt, 2)}; // Process noise matrix
The measurement covariance matrix R is determined based on experience and some trial and error. We are measuring the roll and pitch angles from the accelerometer (i.e. using the direction of the gravity vector) and their respective rates from the gyroscope. Accelerometer data normally contains more noise than gyroscope data so we can broadly say we have more confidence in the gyroscope data. We assume that the state variables are independent so the measurement covariance matrix is also diagonal:
const BLA::Matrix<4, 4> R = {50.0, 0.0, 0.0, 0.0,
0.0, 50.0, 0.0, 0.0,
0.0, 0.0, 10.0, 0.0,
0.0, 0.0, 0.0, 10.0}; // Measurement covariance matrix
The values on the diagonal have been determined by iteratively adjusting R and checking filter performance. We have given larger variance values to the diagonal components corresponding to roll and pitch compared to their rates because we have less confidence in their true value due to sensor noise.
It is worth noting here that these values of Q and R are ones which I found to give satisfactory filter performance (the filter tracks roll and pitch and removes unwanted noise) based on limited testing. These parameters can be further optimised and they will be different for different applications.
Let’s look at how Q_scale_factor and epsilon_max impact filter performance. To illustrate this let’s look at how the filter tracks roll angle without and then with scaling Q. The two plots below show how well the filter tracks roll angle in a level — roll positive — level — roll negative— level manoeuvre.

Without scaling Q the filter is very laggy and gives unacceptable performance. The filter is too confident in the idealised state-space representation of the system (which does not include the outside forces causing the system to rotate) and does not put enough confidence in the measured data.

The situation is improved when continuously scaling Q. The filter now follows the measurement data more closely and does a good job of removing unwanted noise. Remember what we are doing here; we increase Q when the normalised state residual epsilon goes above epsilon_max and reduce it when it goes back below epsilon_max. The following values for epsilon_max and Q_scale_factor were used for scaling Q:
float epsilon_max = 1.0;
float Q_scale_factor = 1000.0;
The filter isn’t perfect. There is still some lag in the filter and the continuous adjustment step has also introduced a kind of “stepping” behaviour as Q is scaled up and down which we can see most prominently in the plot showing roll angle when scaling Q. Further tuning of R, Q and the scaling parameters would result in even better filter performance.
Summary
Building an Arduino-based Kalman filter for attitude determination provides a cost-effective and versatile solution for small-scale applications such as hobby drones. By understanding the theory behind the Kalman filter and implementing it using an Arduino Nano and MPU-6050 motion sensor, you can effectively clean up noisy sensor data and improve attitude estimation. The Kalman filter’s prediction and update steps work together to provide accurate and reliable state estimates. With this knowledge, you can enhance navigation, control, and guidance systems in various fields such as aerospace, robotics, and autonomous vehicles.
The performance of the Kalman filter implemented in this article can be improved with further tuning of the parameters discussed in the Tuning the filter section. Going forward I will look into ways to include the filter implemented in this article in some of my personal projects and I look forward to posting about these here. Hopefully this article has inspired you to try out Kalman filtering too!
Enjoyed reading this article?
Follow and subscribe for more content like this — share it with your network — tell everyone you know how useful Kalman filters are!
Resources
You can access the GitHub repository containing the full PlatformIO project for the Kalman filter here:
If you would like to learn more about Kalman filters, here are some useful resources I referenced while building the filter described in this article:
- https://www.kalmanfilter.net/default.aspx — A guide to Kalman filters with practical examples by Alex Becker. Introduces the theory behind Kalman filters and presents the Kalman filter in matrix notation. Excellent reference for Kalman filter equations.
- https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/ — An illustrated guide to Kalman filters by Tim Babb. Presents a nice description of the measurement and predicted state covariances as being overlapping Gaussian blobs with the true state being somewhere in that overlap.
- https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python — Kalman filter book by Roger Labbe written using Jupyter Notebooks. Lots of great examples including a continuous adjustment Kalman filter.
Let’s Build an Arduino-based Kalman Filter for Attitude Determination was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.