This post ties together the previous three posts.

In this post, I said that an Archimedean spiral has the polar equation

r = b θ1/n

and applied this here to rolls of carpet.

When n = 1, the length of the spiral for θ running from 0 to T is approximately

½ bT²

with the approximation becoming more accurate [1] as T increases.

In this post we want to look at the general case where n might not be 1. In that case the arc length is given by a hypergeometric function, and finding the asymptotic behavior for large T requires evaluating a hypergeometric function at a large argument.

Here’s an example with n = 3.

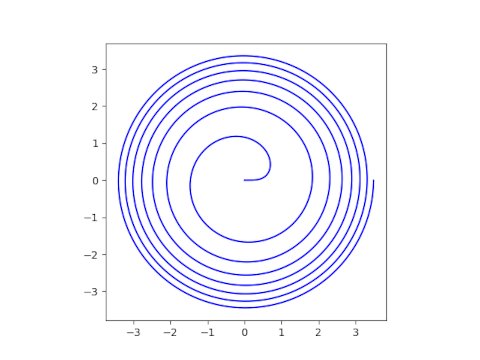
Now the arms are not equally spaced but instead grow closer together.

Arc length

According to MathWorld, the length of the spiral with n > 1 and θ running from 0 to T is given by

L = b T^{1/n} ,_2F_1left(-frac{1}{2}, frac{1}{2n}; 1 + frac{1}{2n}; -n^2 T^2 right)

As I discussed here, the power series defining a hypergeometric function 2F1 diverges for arguments outside the unit disk, but the function can be extended by analytic continuation using the identity

begin{align*} F(a, b; c; z) &= frac{Gamma(c) Gamma(b-a)}{Gamma(b) Gamma(c-a)} ,(-z)^{-aphantom{b}} Fleft(a, 1-c+a; 1-b+a; frac{1}{z}right) \ &+ frac{Gamma(c) Gamma(a-b)}{Gamma(a) Gamma(c-b)} ,(-z)^{-bphantom{a}} Fleft(,b, 1-c+b; 1-a+b; ,frac{1}{z}right) \ end{align*}

Asymptotics

Most of the terms above will drop out in the limit as z = −n²T² gets large. The 1/z terms go to zero, and hypergeometric functions equal 1 when z = 0, and so the F terms on the right hand side above go to 1 as T increases.

In our application the hypergeometric parameters are a = −1/2, b = 1/2n, and c = 1 + 1/2n. The term

(−z)−a  = (−z)1/2

matters, but the term

(−z)−b  = (−z)−1/2n

goes to zero and can be ignored.

We find that

L ≈ k T1 + 1/n

where the constant k is given by

k = bn Γ(1 + 1/2n) Γ(1/2 + 1/2n) / Γ(1/2n) Γ(3/2 + 1/2n)

When n = 1, this reduces to L ≈ ½ bT² as before.

 

[1] The relative approximation error decreases approximately quadratically in T. But the absolute error grows algorithmically.

The post Length of a general Archimedean spiral first appeared on John D. Cook.

Previous Post
Next Post