Pick’s theorem is a surprising and useful to find the area of a region formed by connecting dots on a grid. The area is simply

A = i + p/2 − 1

where i is the number of dots in the interior and p is the number of dots on the perimeter.

Example

For example, the in the figure below there are 11 black dots on the perimeter and 17 blue dots in the interior.

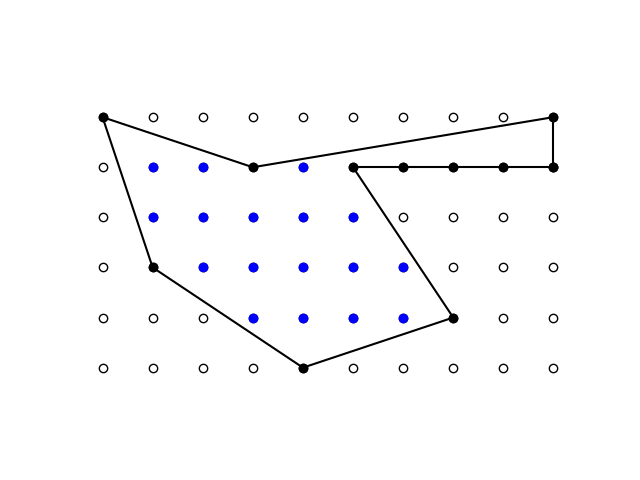
Therefore Pick’s theorem says the area of the figure is 17 + 11/2 − 1 =  21½.

Intuition

It makes sense that the area would be approximately i if the figure is very large. But why do you need to add half the dots on the perimeter and why do you subtract 1?

Pick’s theorem is simple, but it isn’t obvious. If it were obvious, someone closer to the time of Descartes (1596–1650) would have discovered it. Instead, the theorem was discovered by Georg Alexander Pick in 1899. However, the theorem is fairly obvious for a rectangle, and this post will illustrate that case. For a rectangle, you can easily see why you need to add half the perimeter dots and subtract 1.

Rectangular case

Imagine an m by n rectangular array of dots. If you were to draw a frame around those dots with the corners of the rectangle being exactly between dots, the area would be mn, the number of dots inside the frame.

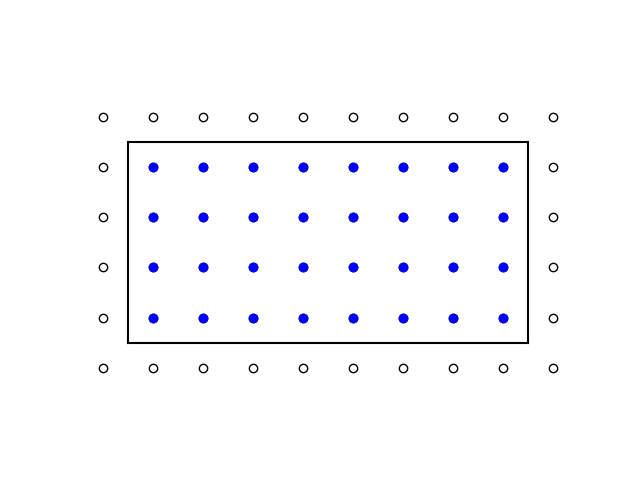
Pick’s theorem does not apply here because the corners of our frame do not lie on the grid. So let’s shift our grid down and to the left so that its corners do lie on the grid.

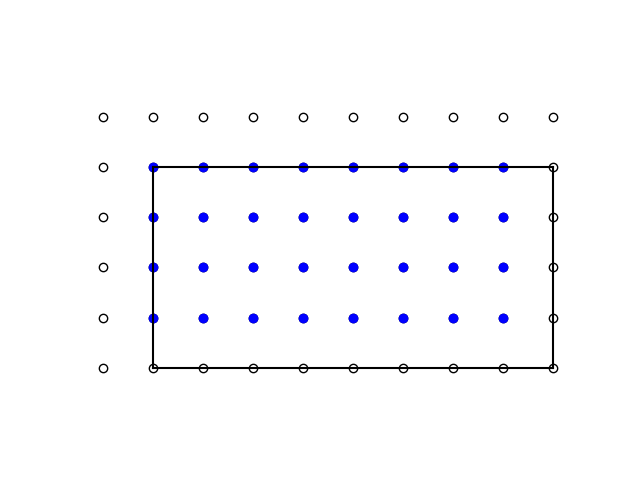
Now some of our original dots, marked in blue, are on the perimeter of the frame. We could add the number of dots on the perimeter to correct for this, but that would be too much because the blue dots on the perimeter are only on the left and top sides. Each has a reflection on the right and bottom, marked with red dots. So we shouldn’t add all the dots on the perimenter, but only half the dots on the perimeter.

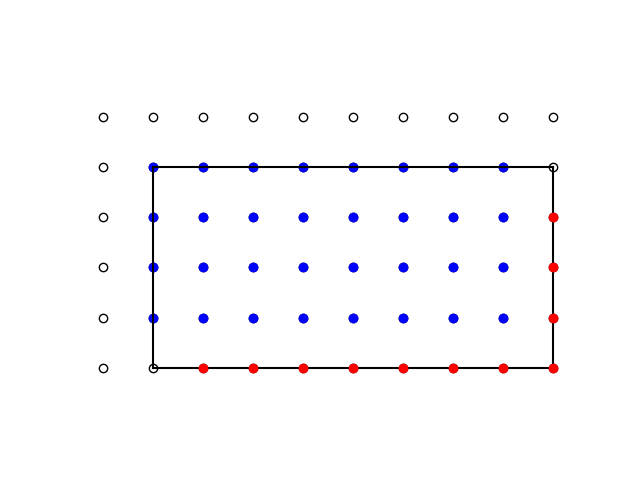
But that still overcounts slightly. There are two dots on the perimeter that do not correspond to a blue dot or to the reflection of a blue dot. These are the hollow circles in the top right and bottom left corners. So when we take half the perimeter, we need to subtract 1 to account for half of this pair of dots.

This doesn’t prove Pick’s theorem in general, but it does prove it for rectangular regions. Even if we can’t see why the formula generalizes to more complicated regions, we can be grateful that it does.

Related posts

The post Intuition for Pick’s Theorem first appeared on John D. Cook.

Previous Post
Next Post