You would think that interpolating at more points would give you a more accurate approximation. There’s a famous example by Runge that proves this is not the case. If you interpolate the function 1/(1 + x²) over the interval [−5, 5], as you add more interpolation points the maximum interpolation error actually increases.
Here’s an example from a post I wrote a few years ago, using 16 interpolation points. This is the same function, rescaled to live on the interval [−1, 1].
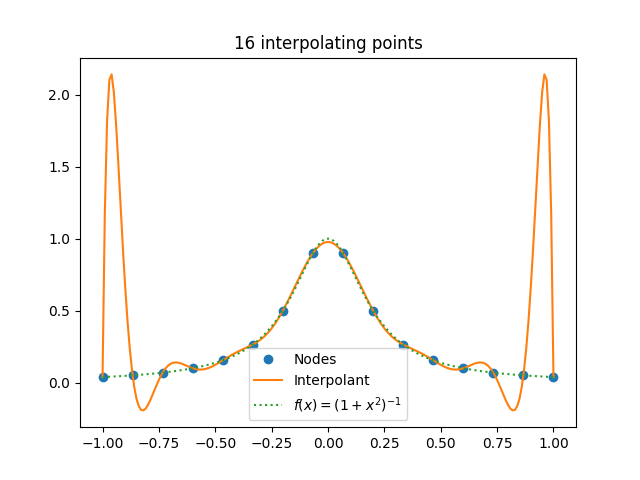
There are two things that make Runge’s example work.
- The interpolation nodes are evenly spaced.
- Singularities in the complex plane too close to the domain.
If you use Chebyshev nodes rather than evenly spaced nodes, the problem goes away.
And if the function being interpolated is analytic in a certain region around the unit inverval (described here) the problem also goes away, at least in theory. In practice, using floating point arithmetic, you can see rapid divergence even though in theory the interpolants converge [1]. That is is point of this post.
Example
So let’s try interpolating exp(−9x²) on the interval [−1, 1]. This function is analytic everywhere, so the interpolating polynomials should converge as the number of interpolation points n goes to infinity. Here’s a plot of what happens when n = 50.
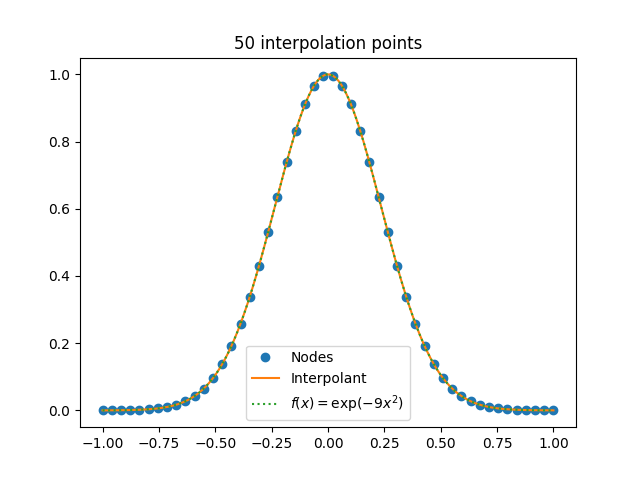
Looks like all is well. No need to worry. But let’s press our luck and try n = 100.
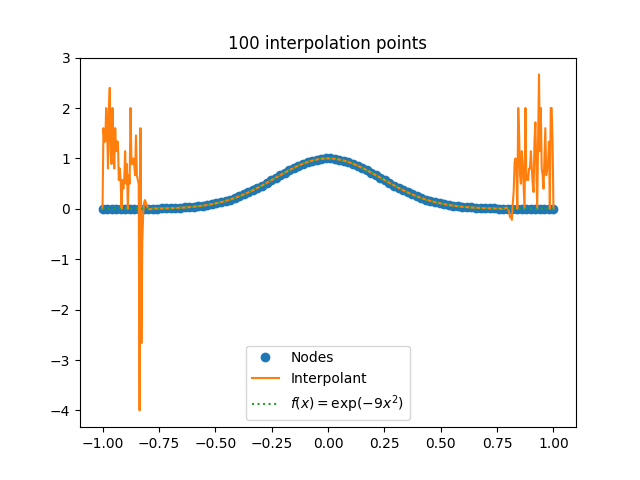
Hmm. Something is wrong.
In fact things are far worse than the plot suggests. The largest interpolant value is over 700,000,000. It just doesn’t show in the plot.
Interpolating at evenly spaced points is badly conditioned. There would be no problem if we could compute with infinite precision, but with finite precision interpolation errors can grow exponentially.
Personal anecdote
Years ago I learned that someone was interpolating exp(−x²) at a large number of evenly spaced points in an application. If memory serves, they wanted to integrate the interpolant in order to compute probabilities.
I warned them that this was a bad idea because of Runge phenomena.
I was wrong on theoretical grounds, because exp(−x²) is analytic. I didn’t know about Runge’s convergence theorem.
But I was right on numerical grounds, because I also didn’t know about the numerical instability demonstrated above.
So I made two errors that sorta canceled out.
Related posts
[1] Approximation Theory and Approximation Practice by Lloyd N. Trefethen
The post Interpolation instability first appeared on John D. Cook.