There are several ways to define an ellipse. If you want to write software draw an ellipse, it’s most convenient to have a parametric form:

begin{align*} x(t) &= h + a cos(theta) cos(t) - b sin(theta) sin(t) \ y(t) &= k + a sin(theta) cos(t) + b cos(theta) sin(t) end{align*}

This gives an ellipse centered at (h, k), with semi-major axis a, semi-minor axis b, and with the major axis rotated by an angle θ from horizontal.

But if you’re going to physically draw an ellipse, there’s a more convenient definition: an ellipse is the set of points such that the sum of the distances to two foci is a constant s. This method is most often called the gardener’s ellipse. It’s also called the nails-and-string method, which is more descriptive.

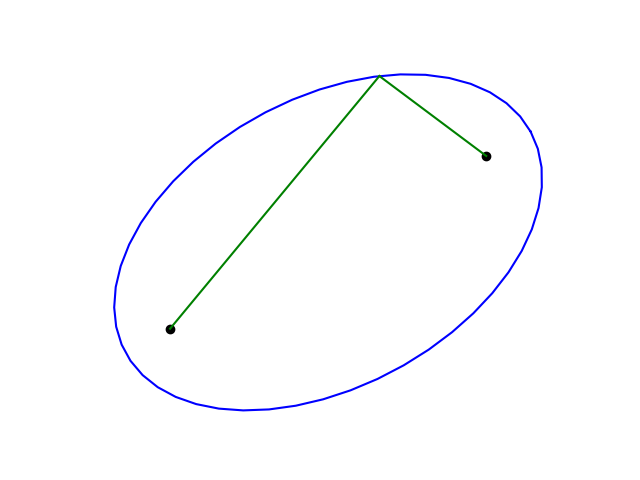
To draw an ellipse on a sheet of plywood, drive a nails in the plywood at both foci, and attach an end of a string of length s to each nail. Then put a pencil in the middle of the string and pull it tight. Keep the string tight as you move the pencil. This will draw an ellipse [1].

Presumably the name gardener’s ellipse comes from the same idea on a larger scale, such as a gardener marking out an elliptical flower bed using two stakes in the ground and some rope.

Going back to drawing on a computer screen, there is a practical use for the gardener’s ellipse: to determine whether a point is inside an ellipse, add the distance from the point to each of the foci of the ellipse. If the sum is less than s then the point is inside the ellipse. If the sum is greater than s the point is outside the ellipse.

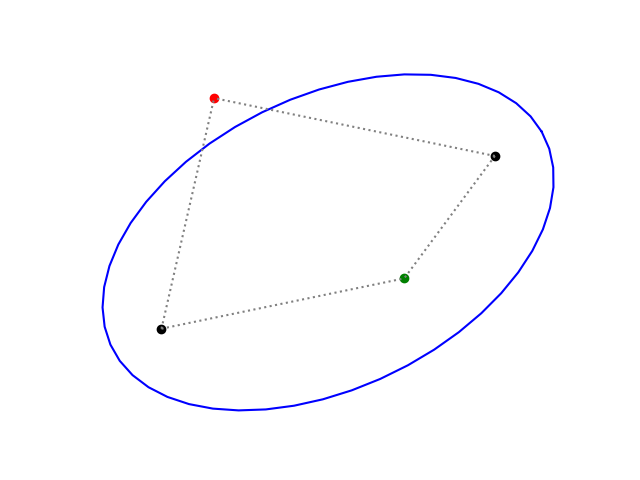
From parameters to nails and string

If you have the parametric form of an ellipse, how do you find the gardener’s method representation?

To make it easier to describe points, set θ = 0 and h = k = 0 for a moment. Then the foci are at (±c, 0) where c² = a² − b².

Since (a, 0) is a point on the string, you have to be able to draw it and so the string must stretch from the focus at (−c, 0) to the point (a, 0) and back to the focus at (c, 0). Therefore the length of the string is 2a.

The length of the string depends on the major axis and not on the minor axis.

When we shift and rotate our ellipse, letting θ, h, and k take on possibly non-zero values, we apply the same transformation to the foci.

begin{align*} F_1 &= (h - ccos(theta), k - csin(theta)) \ F_2 &= (h + ccos(theta), k +, csin(theta)) \ end{align*}

Rotating and translating the ellipse doesn’t change the length of the major axis, so s stays the same.

Related posts

[1] In practice, a carpenter might want to draw an ellipse a different way.

The post Gardener’s ellipse first appeared on John D. Cook.

Previous Post
Next Post