I recently stumbled across the identity

while reading [1]. Here ⌊x⌋ is the floor of x, the largest integer not larger than x.

My first thought was that this was hard to believe. Although the floor function is very simple, its interactions with other functions tends to be complicated. I was surprised that such a simple equation was true.

My second thought was that the equation makes sense. For large n the three terms on the left are roughly equal, and so

Not only that, the approximation gets better as n gets larger. So the theorem is at least plausible.

My third thought was that there is something subtle going on here. Why the 8 on the right hand side? It turns out the theorem is false if you replace the 8 with a 9. Equality fails to hold for n = 0, 3, 8, 15, …

There is a difference between saying x ≈ y and saying ⌊x⌋ = ⌊y⌋. The former makes the latter plausible, but it’s not the same. If x and y are very close, but on opposite sides of an integer, then ⌊x⌋ ≠ ⌊y⌋.

In fact, the approximation

is better when a = 9 than when a = 8. Here’s a plot of the approximation errors.

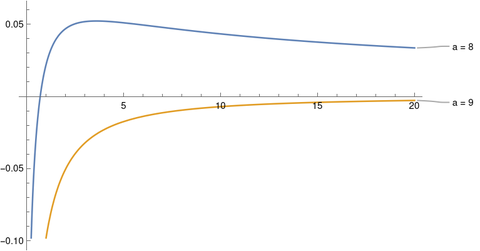
So there’s something clever going on with the selection a = 8.

According to [1], the equation at the top was proposed as a problem in 1988 and a solution was published in 2005. The time span between the proposed theorem and its proof suggests that the proof isn’t trivial, though I have not yet read it.

This is an obscure problem, and so we can’t assume that hundreds of mathematicians were feverishly trying to find a solution for 17 years. On the other hand, if there were a trivial proof it seems someone would have posted it quickly.

[1] Prapanpong Pongsriiam. Analytic Number Theory for Beginners, 2nd edition.. American Mathematical Society 2023

The post Floors and roots first appeared on John D. Cook.