Extending ROS 2 States: An Overview of AICA’s Libraries for State Representation

June 5, 2023
Rss Fetcher

Part 2 of a series of articles centered on ROS 2 and the development we made at AICA to develop a Task and Motion Planning (TAMP) framework

Welcome back to this series of articles centered on the development we made at AICA to develop a Task and Motion Planning (TAMP) framework, extending from ROS 2 features.

In the previous article, we introduced dynamic composition and its current implementation in ROS 2. In this article, we will see the design steps we took to develop a TAMP framework. We will focus here on the motion planning part by showcasing the library we use internally to represent robots and object states. We believe in open source code. Hence, all the libraries we list here are publicly available.

Representing Cartesian States in ROS 2

To plan dynamic robotic actions, the robot needs to have accurate information about its own internal state, as well as the state of its environment. Everything can be represented as a physical moving body observed from a certain point, considered fixed from the observer’s point of view.

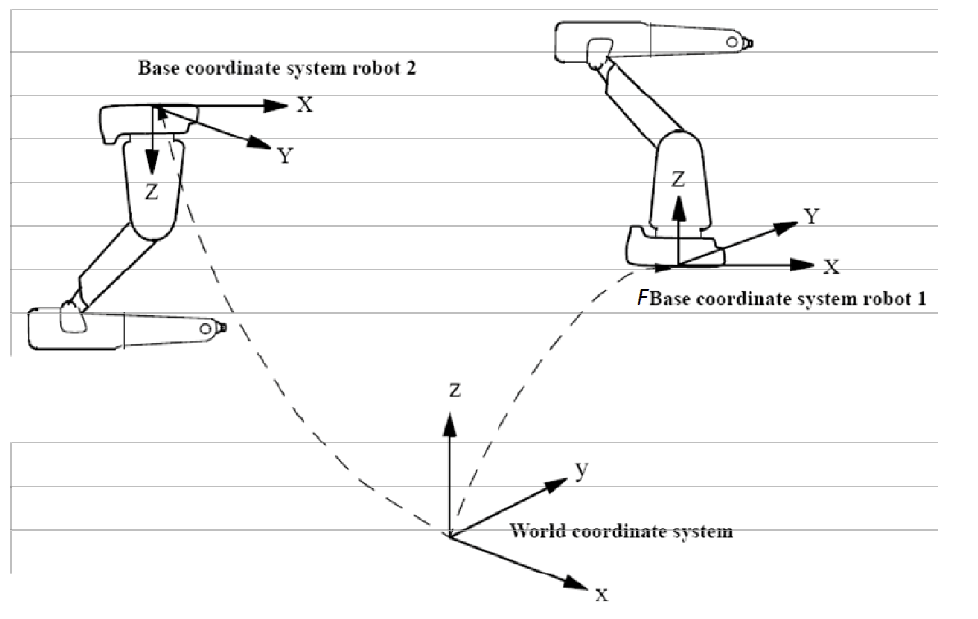
In robotics and physics, the Cartesian state of an object is often described as a reference frame. A reference frame, or coordinate system, is a set of axes used to measure the position and orientation of an object. The choice of reference frame can affect the Cartesian state of the object. For instance, the object’s position and orientation will be different when measured from the perspective of an observer on the ground versus an observer in a moving vehicle.

The object’s orientation is often expressed using a quaternion, a mathematical construct representing a rotation in three-dimensional space. Quaternions are preferred over other representations like Euler angles because they avoid issues like gimbal lock and provide a smooth interpolation between orientations. One important aspect is that most modern libraries provide a translation function between the common representations.

Cartesian representation of two robotic bases expressed in a fixed world reference frame. Image from https://www.tthk.ee/inlearcs/industrial-robot-functionality-and-coordinate-systems/

The Cartesian state can also include the linear and angular velocities, referred to as twist, and the object’s linear and angular accelerations. Those represent the rates of change of the linear and angular velocities, respectively. These quantities are important for understanding the dynamics of the object.

In addition to position, orientation, velocities, and accelerations, the Cartesian state can also include force and torque. Force is a vector quantity that represents the total force acting on the object, while torque is a vector quantity that represents the total torque (or moment) acting on the object. The combined representation of those two elements is referred to as a wrench.

ROS 2 does not provide a unified representation for Cartesian states. Instead, the geometry_msgs package contains several messages that can be grouped to represent a full Cartesian state. Here is an example of how to represent a Cartesian state in ROS 2:

#include "geometry_msgs/msg/pose_stamped.hpp"
#include "geometry_msgs/msg/twist_stamped.hpp"
#include "geometry_msgs/msg/accel_stamped.hpp"
#include "geometry_msgs/msg/wrench_stamped.hpp"

// Create a PoseStamped message to represent the position and orientation
geometry_msgs::msg::PoseStamped pose;
pose.header.frame_id = "world";
pose.pose.position.x = 1.0;
pose.pose.position.y = 2.0;
pose.pose.position.z = 3.0;
pose.pose.orientation = tf2::toMsg(tf2::Quaternion(0.0, 0.0, M_PI/2));

// Create a TwistStamped message to represent the linear and angular velocity
geometry_msgs::msg::TwistStamped twist;
twist.header.frame_id = "world";
twist.twist.linear.x = 0.1;
twist.twist.linear.y = 0.2;
twist.twist.linear.z = 0.3;
twist.twist.angular.x = 0.01;
twist.twist.angular.y = 0.02;
twist.twist.angular.z = 0.03;

// Do the same for AccelStamped and WrenchStamped messages

You would then need to create a custom message that groups those four messages in a single structure. It becomes clear that this is a very tedious and long process. Moreover, more compact representations are available using vectors or quaternions. The Eigen library, for example, is a great way of representing Cartesian states and expressing transformations between them. Lastly, apart from having a compact representation of Cartesian states, the main advantage is considering mathematical operations such as inverting, scaling, and changing reference frame…

In particular, changing the reference frame of a Cartesian state involves transforming the state from one coordinate system to another. This is a common operation in robotics, as different system parts may use different reference frames.

For example, consider a robot arm that is picking up an object. The position and orientation of the object might be described in the reference frame of the robot’s base. However, the control system for the robot’s gripper might use a different reference frame centered on the gripper itself. To control the gripper accurately, we must transform the object’s Cartesian state from the base frame to the gripper frame.

This transformation involves two steps: a translation to account for the difference in position between the two frames and a rotation to account for the difference in orientation.

In ROS 2, these transformations can be performed using the tf2 library, which provides tools for managing multiple coordinate frames and transforming data between them. Here is a simple example:

#include "tf2_geometry_msgs/tf2_geometry_msgs.h"

// Assume we have a PoseStamped msg representing the object's state in the base frame
geometry_msgs::msg::PoseStamped object_state_base;

// And a TransformStamped msg representing the transformation from the base frame to the gripper frame
geometry_msgs::msg::TransformStamped base_to_gripper;

// We can use tf2 to transform the object's state to the gripper frame
geometry_msgs::msg::PoseStamped object_state_gripper;
tf2::doTransform(object_state_base, object_state_gripper, base_to_gripper);

Although this works well for pose (position and orientation), no such tools are available for velocities, accelerations, and wrenches. This motivated us to provide a clear structure to handle Cartesian states (and other types of states) and the transformations between them. Introducing the state_representation library.

Compact Representation of Cartesian States

state_representation is the first library we developed and made publicly available as part of the control-libraries meta-package. It includes multiple representations of states to explain environmental changes (Cartesian, joint state representation of robots, objects shapes, …).

The CartesianState class represents a spatial frame in 3D space containing the following spatial and dynamic properties:

Position
Orientation
Linear velocity
Angular velocity
Linear acceleration
Angular acceleration
Force
Torque

Each state variable is represented as a 3D vector (Eigen::Vector3D), except for the orientation, which is represented by a unit quaternion (Eigen::Quaterniond). The values are assumed to be in standard SI units (meters, radians, seconds, and Newtons).

The spatial properties are expressed relative to a named reference frame. For a CartesianState with the name “A” and reference frame “B,” each state variable represents the instantaneous spatial property measured at or around frame “A” from the perspective of frame “B.” Here is how you can initialize a CartesianState:

#include "state_representation/space/cartesian/CartesianState.hpp"

// Create a CartesianState A expressed in reference frame B
state_representation::CartesianState state("A", "B");

// Set the position
state.set_position(Eigen::Vector3d(1.0, 2.0, 3.0));

// Set the orientation using a quaternion
Eigen::Quaterniond orientation(1.0, 0.0, 0.0, 0.0); // identity quaternion
state.set_orientation(orientation);

// Set the linear velocity
state.set_linear_velocity(Eigen::Vector3d(0.1, 0.2, 0.3));

// Set the angular velocity
state.set_angular_velocity(Eigen::Vector3d(0.01, 0.02, 0.03));

// Do the same for linear & angular accelerations, force and torque

state_representation also provides mathematical operations for changing reference frames. To that extent, we have decided to override the * operator as this is the most common and compact way of representing chained transformations:

// Assume we have a CartesianState 'state_in_A' expressed in frame 'A'
state_representation::CartesianState state_in_A("state", "A");

// And we have a transform from frame 'A' to a new frame 'B'
state_representation::CartesianPose A_in_B("A", "B");

// We can change the reference frame of 'state_in_A' to frame 'B'
state_representation::CartesianState state_in_B = state_in_A * A_in_B;

This operation affects the pose (position and orientation) and all the other state variables (twist, acceleration, and wrench). Other operations, such as addition or difference, are also implemented, as shown below:

#include "state_representation/space/cartesian/CartesianState.hpp"

// Create two CartesianStates
state_representation::CartesianState state1("state1", "world");
state_representation::CartesianState state2("state2", "world");

// Set their positions
state1.set_position(Eigen::Vector3d(1.0, 2.0, 3.0));
state2.set_position(Eigen::Vector3d(4.0, 5.0, 6.0));

// Add the states
state_representation::CartesianState sum = state1 + state2;

// Subtract the states
state_representation::CartesianState difference = state1 - state2;

Those operations are checked for validity. For example, adding states not expressed in the same reference frame will throw an error. We refer the reader to the documentation for additional functionalities, including derived class to express single state variables, time derivation and integration, and norms. Please, note this library is available both in C++ and Python.

From Cartesian to Joint States

One important aspect of robotics lies in the existence of two distinct spaces. As seen above, the Cartesian space represents the state of moving bodies, such as the robot’s end-effector or base. Conversely, the joint state represents the state of the joints of a robot. It typically includes the joint positions (angles for revolute joints or displacements for prismatic joints), velocities (angular or linear), and accelerations. It may also include joint torques or forces.

Following the exact same pattern and API of CartesianState, state_representation provide a JointState class for representing joint states:

#include "state_representation/robot/JointState.hpp"

// Create a JointState for a robot with 7 joints
state_representation::JointState joint_state("my_robot", 7);

// Set the joint positions
joint_state.set_positions(Eigen::VectorXd::Random(7));

// Set the joint velocities
joint_state.set_velocities(Eigen::VectorXd::Random(7));

// Set the joint torques
joint_state.set_torques(Eigen::VectorXd::Random(7));

In this code, we create a JointState for a robot with seven joints, and set the joint positions, velocities, and torques to random values. The accelerations are set to zeroes which are the default values.

One fundamental concept of robotics is the ability to transform Cartesian space into joint space and vice versa. Knowing the robot’s state, one can infer the Cartesian state of each robot’s body part. This can be achieved for all state variables of both states.

Implementing Kinematics and Dynamics

Kinematics is the study of motion without considering the forces that cause the motion. In robotics, kinematics involves the mathematical description of the motion of robots. There are two primary types of kinematics: direct (or forward) kinematics and inverse kinematics.

On the other hand, dynamics involves studying forces and torques that cause motion in robots. Similar to kinematics, dynamics can be divided into two types: direct (or forward) dynamics and inverse dynamics.

Direct (forward) kinematics

Direct kinematics is the process of determining the position and orientation of the end-effector (the robot’s tool or hand) given the robot’s joint angles and lengths. In other words, if you know the angles of all the joints in the robot, forward kinematics allows you to calculate where the end-effector is.

The mathematical model that describes this relationship is often represented as a function that maps joint variables (angles for revolute joints, displacements for prismatic joints) to a pose in Cartesian space (position and orientation).

Inverse kinematics

Inverse kinematics is the reverse process of direct kinematics. Given a desired pose of the end-effector, inverse kinematics determines the joint angles and lengths that would achieve that position. In other words, if you want the robot to reach a certain location, inverse kinematics tells you how to position and orient each robot’s joints.

Inverse kinematics is often more complex than direct kinematics because there may be multiple sets of joint angles that result in the same end-effector position (multiple solutions), or there may need to be a way to position the joints to reach the desired location (no solution).

Both direct and inverse kinematics are fundamental to robot motion planning and control. Direct kinematics is often used in robot simulation and visualization, while inverse kinematics is used in path planning and control, where the goal is to move the end-effector to a desired location.

Direct (forward) dynamics

Direct dynamics is the process of determining the robot’s acceleration given the joint torques (or forces for prismatic joints) and the current state of the robot (joint positions and velocities). In other words, if you know the forces applied to the robot and its current state, forward dynamics allow you to calculate how the robot will move.

The mathematical model that describes this relationship is often represented as a function that maps joint torques and the current state to joint accelerations. This function is typically derived from the robot’s equations of motion, which are based on Newton’s second law of motion (force equals mass times acceleration).

Inverse dynamics

Inverse dynamics is the reverse process of direct dynamics. Given the desired motion of the robot (joint positions, velocities, and accelerations), inverse dynamics determines the joint torques that would achieve that motion. In other words, if you want the robot to move a certain way, inverse dynamics tells you how much force or torque to apply at each joint.

Inverse dynamics is often more complex than direct dynamics because it involves calculating the forces and torques required to overcome inertia, gravity, and damping. However, it is a crucial part of robot control, as it allows the control system to command the appropriate forces and torques to achieve the desired motion.

Both direct and inverse dynamics are fundamental to robot motion planning and control. Direct dynamics is often used in robot simulation, where the goal is to predict how the robot will move given certain forces. Inverse dynamics is used in robot control, where the goal is to command the robot to move in a certain way.

Using Pinocchio

To compute both kinematics and dynamics, we rely on the open-source library pinocchio. It is written in C++ and is designed to be fast and flexible. To get information on the robot (segment length, body masses, etc.), the library relies on URDF models commonly used in ROS / ROS 2.

We have developed a wrapper around it in the robot_model library. This library is fully integrated with CartesianState and JointState from state_representation. We use it to convert spaces while we develop controllers.

For example, it provides simple-to-use functions for forward and inverse kinematics:

// initialize the robot model from a URDF
robot_model::Model model("myrobot", "path/to/urdf/myrobot.urdf")

// forward kinematics: pose of end-effector frame from the robot joint positions
state_representation::JointPositions jp = state_representation::JointPositions::Random("myrobot", 7);
state_representation::CartesianPose pose = model.forward_kinematics(jp);

// inverse kinematics: joint positions from end-effector pose
state_representation::CartesianPose cp = state_representation::CartesianPose::Random("eef");
state_representation::JointPositions jp = model.inverse_kinematics(cp);

// forward velocity kinematics: twist of end-effector frame from the robot joint velocities and positions
state_representation::JointState js = state_representation::JointState::Random("myrobot", 7);
state_representation::CartesianTwist twist = model.forward_velocity(js);

// inverse velocity kinematics: joint velocities from end-effector twist and current state of the robot
state_representation::CartesianTwist ct = state_representation::CartesianTwist::Random("eef");
state_representation::JointPositions jp = state_representation::JointPositions::Random("myrobot", 7);
state_representation::JointVelocities jv = model.inverse_velocity(ct, jp);

and also forward and inverse dynamics:

// inertia matrix from joint positions
state_representation::JointPositions jp = state_representation::JointPositions::Random("myrobot", 7);
Eigen::MatrixXd inertia = model.compute_inertia_matrix(jp);
// inertia torques, equivalent to inertia multiplied by joint accelerations. The joint positions part of the state
// is used to compute the inertia matrix
state_representation::JointState js = state_representation::JointState::Random("myrobot", 7);
state_representation::JointTorques inertia_t = model.compute_inertia_torques(js);

// coriolis matrix from joint positions and velocities
state_representation::JointState js = state_representation::JointState::Random("myrobot", 7);
Eigen::MatrixXd coriolis = model.compute_coriolis_matrix(js);
// coriolis torques, equivalent to coriolis multiplied by joint velocities. The joint positions part of the state
// is used to compute the coriolis matrix
state_representation::JointState js = state_representation::JointState::Random("myrobot", 7);
state_representation::JointTorques coriolis_t = model.compute_coriolis_torques(js);

// gravity torques from joint positions
state_representation::JointPositions jp = state_representation::JointPositions::Random("myrobot", 7);
state_representation::JointTorques gravity_t = model.compute_gravity_torques(jp);

Although dynamics computations are available, these are not used as much as kinematics in practice. One of the main reasons is that robot manufacturers treat inertia and mass data as trade secrets; even if they provide them, they are sometimes inaccurate. However, there are new techniques to learn those data from direct interaction. We are looking at this to improve those models and achieve a finer level of control for force-based applications.

Conclusion

In this article, we have seen how the state of the robot and its environment can be represented using Cartesian and joint states. We have hinted at how both spaces can be transformed and their relationships. We also introduced the libraries we developed at AICA to handle those transformations.

The state_representation and robot_model libraries are designed to be highly versatile and easy to use. They extend the representation of states that can be found in ROS / ROS 2 and rely on modern and efficient libraries for computation (such as Eigen and pinocchio). Both libraries can be installed from the control-libraries meta-package and provide C++ and Python implementations.

Looking at control-libraries, you will notice two additional libraries, dynamical_systems and controllers that were not addressed in this article. This will be the focus of the next article, which will cover the topics of motion planning and control strategies based on the representation of states introduced here. Stay tuned for more insights on robotics!

References

Extending ROS 2 States: An Overview of AICA’s Libraries for State Representation was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.