The previous post mentioned that 24! ≈ 1024 and 25! ≈ 1025.
For every n, there is some base b such that n! = bn. For example, 30! ≈ 1230.
It’s easy to find b:
What’s interesting is that b is very nearly a linear function of n.
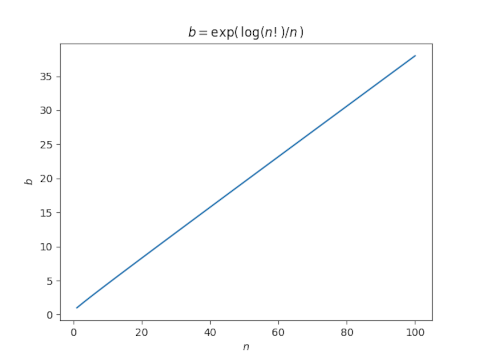
In hindsight it’s clear that this should be the case—it follows easily from Stirling’s approximation—but I didn’t anticipate this before I plotted it.
Now fix n and find b such that n! = bn. Since the relationship between n and b(n) is nearly linear, this suggests
which is true. It follows from the multiplication identity for the gamma function:
![]()
Let z = n + 1/2 so that the left side is (2n)!. On the right side, Γ(z + 1/2) = n! and Γ(z) is not too different from n!. The rest of the right side is 22n/√π.
So our observation that b(n) is nearly linear gave us a hint of Gauss’s multiplication formula.
The post Every factorial is a power first appeared on John D. Cook.