Yesterday I wrote about the equation of a circle through three points. This post will be similar, looking at the equation of an ellipse or hyperbola through five points. As with the earlier post, we can write down an elegant equation right away. Making the equation practical will take more work.

The equation of a general conic section through five points

begin{vmatrix} x^2 & y^2 & xy & x & y & 1 \ x_1^2 & y_1^2 & x_1 y_1 & x_1 & y_1 & 1 \ x_2^2 & y_2^2 & x_2 y_2 & x_2 & y_2 & 1 \ x_3^2 & y_3^2 & x_3 y_3 & x_3 & y_3 & 1 \ x_4^2 & y_4^2 & x_4 y_4 & x_4 & y_4 & 1 \ x_5^2 & y_5^2 & x_5 y_5 & x_5 & y_5 & 1 \ end{vmatrix} = 0

Direct but inefficient solution

The most direct (though not the most efficient) way to turn this into an equation

Ax^2 + By^2 + Cxy + Dx + Ey + F = 0

is to expand the determinant by minors of the first row.

A = begin{vmatrix} y_1^2 & x_1 y_1 & x_1 & y_1 & 1 \ y_2^2 & x_2 y_2 & x_2 & y_2 & 1 \ y_3^2 & x_3 y_3 & x_3 & y_3 & 1 \ y_4^2 & x_4 y_4 & x_4 & y_4 & 1 \ y_5^2 & x_5 y_5 & x_5 & y_5 & 1 \ end{vmatrix} ,, B = - begin{vmatrix} x_1^2 & x_1 y_1 & x_1 & y_1 & 1 \ x_2^2 & x_2 y_2 & x_2 & y_2 & 1 \ x_3^2 & x_3 y_3 & x_3 & y_3 & 1 \ x_4^2 & x_4 y_4 & x_4 & y_4 & 1 \ x_5^2 & x_5 y_5 & x_5 & y_5 & 1 \ end{vmatrix}

C = begin{vmatrix} x_1^2 & y_1^2 & x_1 & y_1 & 1 \ x_2^2 & y_2^2 & x_2 & y_2 & 1 \ x_3^2 & y_3^2 & x_3 & y_3 & 1 \ x_4^2 & y_4^2 & x_4 & y_4 & 1 \ x_5^2 & y_5^2 & x_5 & y_5 & 1 \ end{vmatrix} ,, D = - begin{vmatrix} x_1^2 & y_1^2 & x_1 y_1 & y_1 & 1 \ x_2^2 & y_2^2 & x_2 y_2 & y_2 & 1 \ x_3^2 & y_3^2 & x_3 y_3 & y_3 & 1 \ x_4^2 & y_4^2 & x_4 y_4 & y_4 & 1 \ x_5^2 & y_5^2 & x_5 y_5 & y_5 & 1 \ end{vmatrix}

E = begin{vmatrix} x_1^2 & y_1^2 & x_1 y_1 & x_1 & 1 \ x_2^2 & y_2^2 & x_2 y_2 & x_2 & 1 \ x_3^2 & y_3^2 & x_3 y_3 & x_3 & 1 \ x_4^2 & y_4^2 & x_4 y_4 & x_4 & 1 \ x_5^2 & y_5^2 & x_5 y_5 & x_5 & 1 \ end{vmatrix} ,, F = - begin{vmatrix} x_1^2 & y_1^2 & x_1 y_1 & x_1 & y_1\ x_2^2 & y_2^2 & x_2 y_2 & x_2 & y_2\ x_3^2 & y_3^2 & x_3 y_3 & x_3 & y_3\ x_4^2 & y_4^2 & x_4 y_4 & x_4 & y_4\ x_5^2 & y_5^2 & x_5 y_5 & x_5 & y_5\ end{vmatrix}

More efficient solution

It would be much more efficient to solve a system of equations for the coefficients. Since the determinant at the top of the page is zero, the columns are linearly dependent, and some linear combination of those columns equals the zero vector. In fact, the coefficients of such a linear combination are the coefficients A through F that we’re looking for.

We have an unneeded degree of freedom since any multiple of the coefficients is valid. If we divide every coefficient by A, then the new leading coefficient is 1. This gives us five equations in five unknowns.

begin{bmatrix} y_1^2 & x_1 y_1 & x_1 & y_1 & 1 \ y_2^2 & x_2 y_2 & x_2 & y_2 & 1 \ y_3^2 & x_3 y_3 & x_3 & y_3 & 1 \ y_4^2 & x_4 y_4 & x_4 & y_4 & 1 \ y_5^2 & x_5 y_5 & x_5 & y_5 & 1 \ end{bmatrix} begin{bmatrix} B \ C \ D \ E \ F \ end{bmatrix} = - begin{bmatrix} x_1^2 \ x_2^2 \ x_3^2 \ x_4^2 \ x_5^2 \ end{bmatrix}

Python example

The following code will generate five points and set up the system of equations Ms = b whose solution s will give our coefficients.

    import numpy as np

    np.random.seed(20230619)

    M = np.zeros((5,5))
    b = np.zeros(5)
    for i in range(5):
        x = np.random.random()
        y = np.random.random()    
        M[i, 0] = y**2
        M[i, 1] = x*y
        M[i, 2] = x
        M[i, 3] = y
        M[i, 4] = 1
        b[i] = -x*x

Now we solve for the coefficients.

    s = np.linalg.solve(M, b)
    A, B, C, D, E, F = 1, s[0], s[1], s[2], s[3], s[4]

Next we verify that the points we generated indeed lie on the conic section whose equation we just found.

    for i in range(5):
        x = M[i, 2]
        y = M[i, 3]
        assert( abs(A*x*x + B*y*y + C*x*y + D*x + E*y + F) < 1e-10 )

Ellipse or hyperbola?

It turns out that the five points generated above lie on a hyperbola.

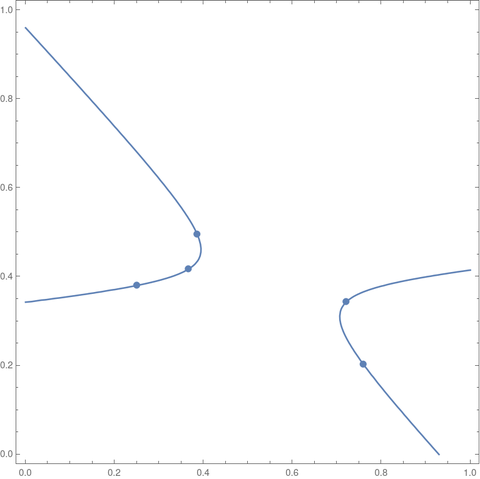
If we had set the random number generator seed to 20230620 we would have gotten an ellipse.

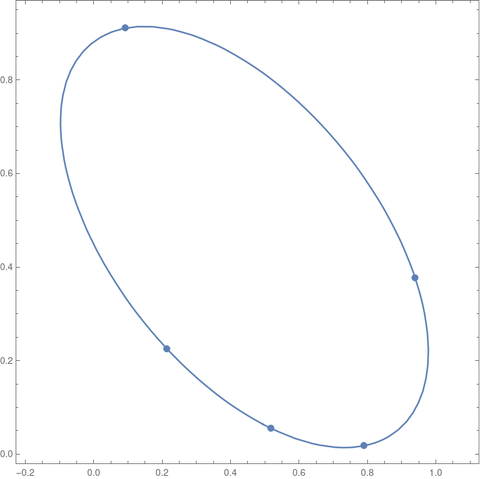
When we generate points at random, as we did above, we will almost certainly get an ellipse or a hyperbola. Since we’re generating pseudorandom numbers, there is some extremely small chance the generated points would lie on a line or on a parabola. In theory, this almost never happens, in the technical sense of “almost never.”

If 4AB − C² is positive we have a an ellipse. If it is negative we have a hyperbola. If it is zero, we have a parabola.

Related posts

The post Equation of an ellipse or hyperbola through five points first appeared on John D. Cook.

Previous Post
Next Post