Dan Piponi posted a chart like the one below on Mastodon.

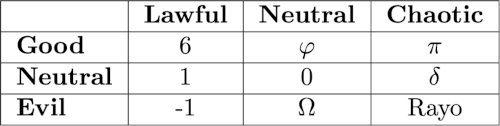
At the risk of making a joke not funny by explaining it, I’d like to explain Dan’s table.

The alignment matrix above comes from Dungeons & Dragons and has become a kind of meme.

The number neutral good number φ is the golden ratio, (1 + √5)/2 = 1.6180339….

Presumably readers of this blog have heard of π. Perhaps it ended up in the chaotic column because it is believed to be (but hasn’t been proven to be) a “normal number,” i.e. the distribution of its digits are normal when expressed in any base.

The number δ = 4.6692016… above is Feigenbaum’s constant, something I touched on three weeks ago. I suppose putting it in the chaos column is a kind of pun because the number comes up in chaos theory. It is believed that δ is transcendental, but there’s no proof that it’s even irrational.

The number Ω is Chaitin’s constant. In some lose sense, this number is the probability that a randomly generated program will halt. It is a normal number, but it is also uncomputable. The smallest program to compute the first n bits of Ω must have length O(n) and so no program of any fixed length can crank out the bits of Ω.

Rayo’s number is truly evil. It is said to be the largest named number. Here’s the definition:

The smallest number bigger than any finite number named by an expression in any language of first-order set theory in which the language uses only a googol symbols or less.

You could parameterize Rayo’s definition by replacing googol (= 10¹⁰⁰) with an integer n. The sequence Rayo(n) starts out small enough. According to OEIS Rayo(30) = 2 because

the 30 symbol formula “(∃x_1(x_1∈x_0)∧(¬∃x_1(∃x_2((x_2∈x_1∧x_1∈x_0)))))” uniquely defines the number 1, while smaller formulae can only define the number 0, the smallest being the 10 symbol “(¬∃x_1(x_1∈x_0))”.

OEIS does not give the value of Rayo(n) for any n > 30, presumably because it would be very difficult to compute even Rayo(31).

The post Dungeons, Dragons, and Numbers first appeared on John D. Cook.