Years ago I wrote about how you can make a decent approximation to the Gaussian density by shifting and scaling the cosine function. This observation dates back at least as far as 1961.
Turns out you can do even better by raising the cosine term to a power. Not only can you get a good approximation, you can get an upper and lower bound of the same form.
In [1] the authors prove the following. For −π/2 < x < π/2,
and
with the best possible constants
When the authors say “best” they mean best with respect to L2 norm, i.e. best the the least-squares sense.
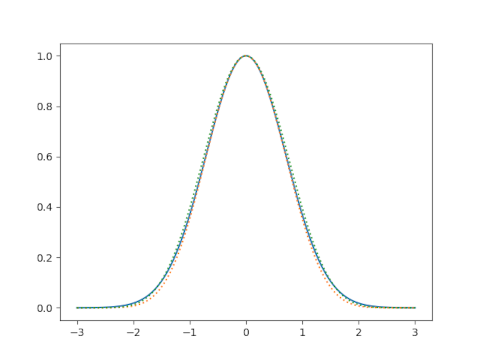
The graph at the top of the page plots exp(−x²) as solid blue line, the first upper bound as a dotted green line, and the first lower bound as a dotted orange line. The blue and green lines blend into a single bluish-green line. You can barely see the orange line separate from the others. The curves are difficult to distinguish visually, which is the point.
The second pair of upper and lower bounds are even better. Here’s a plot of the errors for the second pair of bounds.
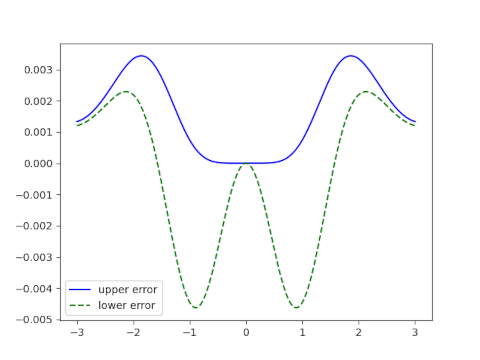
Note that the theorem is stated for the interval [−π/2, π/2], but the plot covers a wider range in order to show that the errors are still small outside the interval. Outside the specified interval, the lower bound error becomes positive, i.e. the lower bound is no longer a lower bound, though it’s still a good approximation.
[1] Yogesh J. Bagul and Christophe Chesneau. Some sharp circular and hyperbolic bounds of exp(−x²) with applications. Applicable Analysis and Discrete Mathematics, Vol. 14, No. 1 (April 2020), pp. 239–254
The post Cosine power approximation to Gaussian density first appeared on John D. Cook.