The Dixon elliptic functions sm and cm are in some ways analogous to sine and cosine. However, whereas sine and cosine satisfy
the Dixon functions satisfy
The exponent 3 foreshadows the fact that these functions have a sort of three-fold symmetry. In particular, the function sm maps an equilateral triangle in the complex plane to the unit circle. The function sm gives a conformal map from the interior of this circle to the interior of the unit disk.
In this post we will work with sm−1 rather than sm, mapping the unit circle to an equilateral triangle. An advantage of working with the inverse function is that we can start with the unit circle and see what triangle it maps to; if we started with the triangle it might seem arbitrary. Also, the function sm is not commonly part of mathematical software libraries—it’s not in Mathematica or SciPy—but you can compute its inverse via
using the hypergeometric function 2F1, which is a common part of mathematical libraries.
The following image shows concentric circles in the z plane and their image under sm−1 in the w plane, w = sm−1(z).
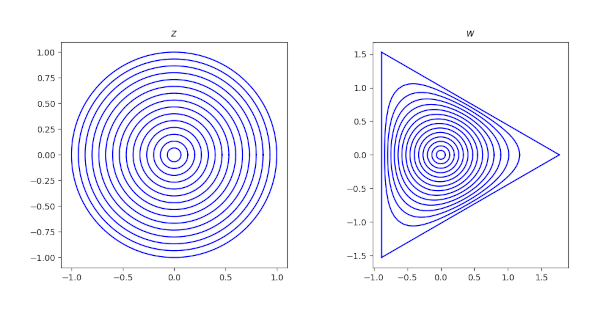
If we were to use this in applications, we’d need to know the vertices of the image triangle so we could do a change of variables to transform this triangle into a particular triangle we’re interested in.
The centroid of the image is at the origin, and the right-most vertex is at approximately 1.7666. To be exact, the vertex is at
v = ⅓ B(⅓, ⅓)
where B is the beta function. (Notice all the 3’s in the formula for v.) The other two vertices are at exp(2π/3)v and exp(4πi/3) v.
One way this conformal map could arise in practice is solving Laplace’s equation on a triangle. You can solve Laplace’s equation on a disk in closed form, and transform that solution into a solution on the triangle.
Related posts
The post Conformal map between disk and equilateral triangle first appeared on John D. Cook.