Given the equations for two circles, how can you tell whether they intersect? And if they do intersect, how do you find the point(s) of intersection?

MathWorld gives a derivation, but I’d like to add the derivation there in two ways. First, I’d like to be more explicit about the number of solutions. Second, I’d like to make the solution more general.

The derivation begins with the simplifying assumption that one circle is centered at the origin and the other circle is centered somewhere along the x-axis. You can always change coordinates so that this is the case, and doing so simplifies the presentation. Undoing this simplification is implicitly left as an exercise to the reader. I will go through this exercise here because I want a solution I can use in software.

Finding the x coordinate

Suppose the first circle, the one centered at the origin, has radius R. The other circle is centered at (d, 0) for some d, and has radius r. The  x-coordinate of the intersection is shown to satisfy the following equation.

x = frac{d^2 -r^2 + R^2}{2d}

When I got to this point in the derivation I was wondering what assumption was made that guaranteed there is a solution. Clearly if you increase d enough, moving the second circle to the right, the circles won’t intersect. And yet the derivation for x always succeeds, unless d = 0. If d does equal 0, the two circles are concentric. In that case they’re the same circle if R = r; otherwise they never intersect.

Finding the y coordinate

Why does the derivation for x always succeed even though the intersection might be empty? The resolution depends on the solution for y. What we’ve found is that if the circles intersect, the x coordinate of the point(s) of intersection is given by the equation above.

The y coordinate of the point(s) of intersection satisfies

begin{align*} y^2 &= frac{4d^2R^2 - (d^2 - r^2 + R^2)^2}{4d^2} \ &= frac{(-d+r-R)(-d-r+R)(-d+r+R)(d+r+R)}{4d^2} end{align*}

If the numerator is negative, there is no real solution, no intersection. If the numerator is zero, there is one solution, and the two circles are tangent. if the numerator is positive, there are two solutions.

The distance between the two intersection points, if there are two intersection points, is a = 2|y|. This will be needed below.

a = frac{sqrt{(-d+r-R)(-d-r+R)(-d+r+R)(d+r+R)}}{d}

General position

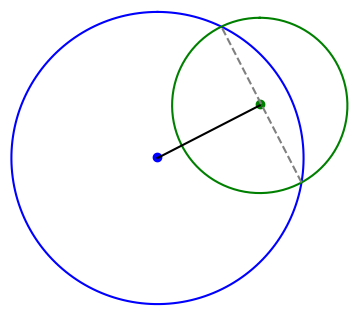
Now suppose we’re first circle is centered at (x0, y0) and the second circle is centered at (x1, y1). Again we let d be the distance between the centers of the circles. The circles intersect twice if d < R + r, once if d = R + r, and never if d > R + r.

Imagine for a moment shifting and rotating the plane so that (x0, y0) goes to the origin and goes to (d, 0). The length of the line segment between the two intersection points is still given by a above. And the distance from the center of the first circle to that line segment is given by the equation for x above.

So to find the points of intersection, we first form a unit vector in the direction of the center of the first circle headed toward the center of the second circle. This is the black line at the top of the post. We move a distance x along this line, with x as in the equation above, and then move perpendicularly a distance a/2 in either direction. This is the dashed gray line.

Python code

The following code implements the algorithm described above.

    def circle_intersect(x0, y0, r0, x1, y1, r1):
        c0 = np.array([x0, y0])
        c1 = np.array([x1, y1])
        v = c1 - c0
        d = np.linalg.norm(v)
    
        if d > r0 + r1 or d == 0:
            return None
        
        u = v/np.linalg.norm(v)
        xvec = c0 + (d**2 - r1**2 + r0**2)*u/(2*d)
    
        uperp = np.array([u[1], -u[0]])
        a = ((-d+r1-r0)*(-d-r1+r0)*(-d+r1+r0)*(d+r1+r0))**0.5/d
        return (xvec + a*uperp/2, xvec - a*uperp/2)

The post Calculating the intersection of two circles first appeared on John D. Cook.

Previous Post
Next Post