Midjourney: Cubic matrix multiplication

Years ago, I wrote an implementation of the Strassen matrix multiplication algorithm in C++, and recently re-implemented it in Rust as I continue to learn the language. This was a useful exercise in learning about Rust performance characteristics and optimization techniques, because although the algorithmic complexity of Strassen is superior to the naive approach, it has a high constant factor from the overhead of allocations and recursion within the algorithm’s structure.

The general algorithm

The general (naive) matrix multiplication algorithm is the three nested loops approach everyone learns in their first linear algebra class, which most will recognize as O(n³)

pub fn 
mult_naive (a: &Matrix, b: &Matrix) -> Matrix {
    if a.rows == b.cols {
        let m = a.rows;
        let n = a.cols;

        // preallocate
        let mut c: Vec<f64> = Vec::with_capacity(m * m);

        for i in 0..m {
            for j in 0..m {
                let mut sum: f64 = 0.0;
                for k in 0..n {
                    sum += a.at(i, k) * b.at(k, j);
                }

                c.push(sum);
            }
        }

        return Matrix::with_vector(c, m, m);
    } else {
        panic!("Matrix sizes do not match");
    }
}

This algorithm slow not just because of the three nested loops, but because the inner-loop traversal of B by columns via b.at(k, j) rather than by rows is terrible for CPU cache hit rate.

Transposition for better performance

The transposed-naive approach reorganizes the multiplication strides of matrix B into a more cache-favorable format by allowing multiplications iterations over B run over rows rather than columns. Thus A x B turns into A x B^t

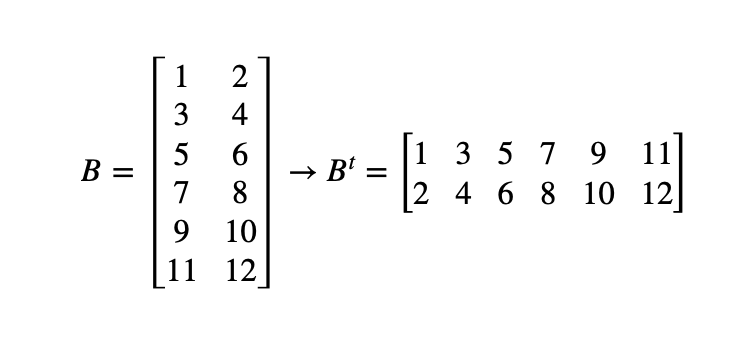
It involves a new matrix allocation (in this implementation, anyways) and a complete matrix iteration (an O(n²) operation, meaning more precisely this approach is O(n³) + O(n²)) — I will show further down how much better it performs. It looks like the following:

fn multiply_transpose (A: Matrix, B: Matrix):
  C = new Matrix(A.num_rows, B.num_cols)

  // Construct transpose; requires allocation and iteration through B
  B’ = B.transpose()

  for i in 0 to A.num_rows:
    for j in 0 to B'.num_rows:
      sum = 0;
      for k in 0 to A.num_cols:
        // Sequential access of B'[j, k] is much faster than B[k, j]
        sum += A[i, k] * B'[j, k]
      C[i, j] = sum
  return C

Sub-cubic: How the Strassen algorithm works

To understand how Strassen’s algorithm works (code in Rust here), first consider how matrices can be represented by quadrants. To conceptualize what this looks like:

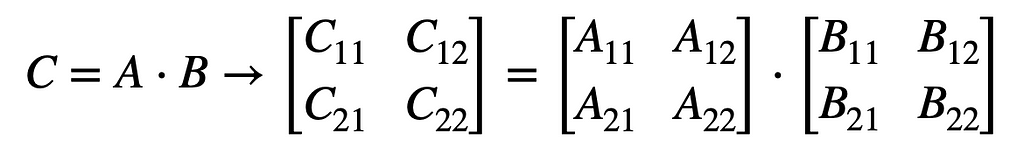
Using this quadrant model in the naive algorithm, each of the four quadrants of the result matrix C is the sum of two sub-matrix products, resulting in 8 multiplications total.

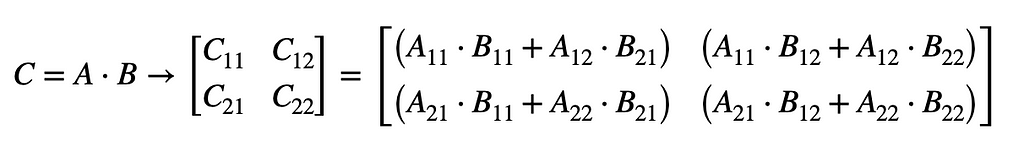
Considering these eight multiplications, each of which operates on a block matrix with a row and column span of about half the size of A and B, the complexity works out to the same:

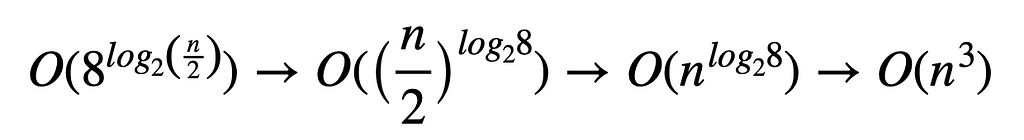
Strassen’s algorithm defines seven intermediate block matrices composed from these quadrants:

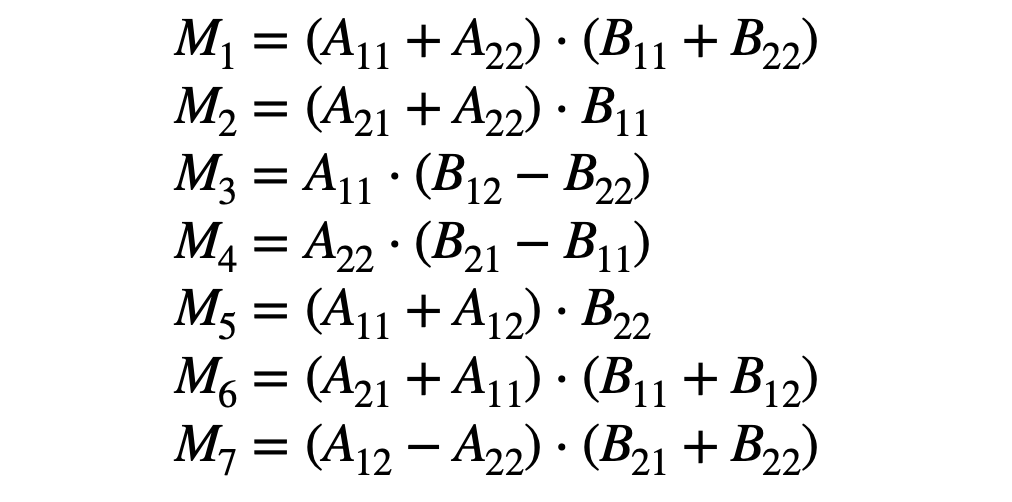
Which are calculated through only 7 multiplications, rather than 8. These multiplications can be recursive Strassen multiplications, and can be used to compose the final matrix as such:

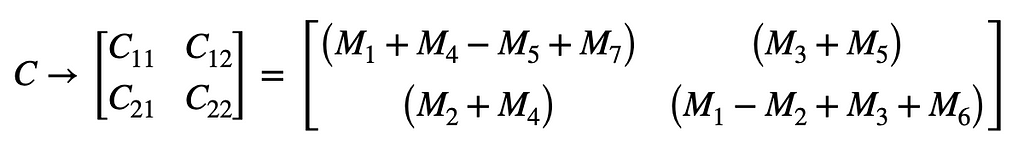
With the resulting sub-cubic complexity:

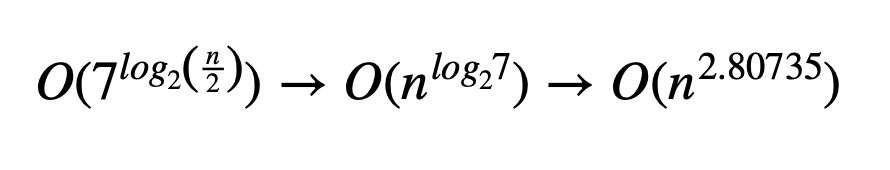
Parallelism

The computation of the intermediate matrices M1 … M7 is an embarrassingly parallel problem, so it was easy to instrument a concurrent variant of the algorithm as well (once you begin to understand Rust’s rules around closures).

/**
 * Execute a recursive strassen multiplication of the given vectors, 
 * from a thread contained within the provided thread pool.
 */
fn 
_par_run_strassen (a: Vec<f64>, b: Vec<f64>, 
                   m: usize, pool: &ThreadPool) 
                     -> Arc<Mutex<Option<Matrix>>> {
    let m1: Arc<Mutex<Option<Matrix>>> = Arc::new(Mutex::new(None));
    let m1_clone = Arc::clone(&m1);
     
    pool.execute(move|| { 
        // Recurse with non-parallel algorithm once we're 
        // in a working thread
        let result = mult_strassen(
            &mut Matrix::with_vector(a, m, m),
            &mut Matrix::with_vector(b, m, m)
        );
        
        *m1_clone.lock().unwrap() = Some(result);
    });

    return m1;
}

Benchmarking

I wrote a some quick benchmarking code, which runs each of the four algorithms for a few trials on an increasing range of matrix dimensions, and reports the average time for each.

~/code/strassen ~>> ./strassen --lower 75 --upper 100 --factor 50 --trials 2

running 50 groups of 2 trials with bounds between [75->3750, 100->5000]

x    y    nxn      naive       transpose  strassen   par_strassen
75   100  7500     0.00ms      0.00ms     1.00ms     0.00ms
150  200  30000    6.50ms      4.00ms     4.00ms     1.00ms
225  300  67500    12.50ms     9.00ms     8.50ms     2.50ms
300  400  120000   26.50ms     22.00ms    18.00ms    5.50ms
[...]
3600 4800 17280000 131445.00ms 53683.50ms 21210.50ms 5660.00ms
3675 4900 18007500 141419.00ms 58530.00ms 28291.50ms 6811.00ms
3750 5000 18750000 154941.00ms 60990.00ms 26132.00ms 6613.00ms

I then visualized results via pyplot :

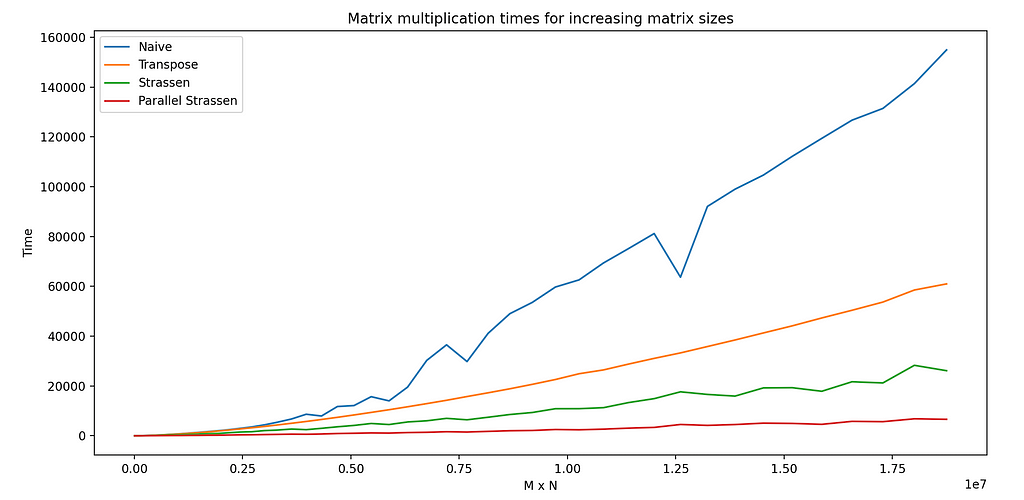
This graph demonstrates multiplication times of matrices from 7.5k elements (N x M = 75 x 100) up to about 19 million (N x M = 3750 x 5000). You can see how quickly the naive algorithm becomes computationally impractical, taking two and a half minutes at the high end.

The Strassen algorithm, by comparison, scales more smoothly, and the parallel algorithm computes the results for two matrices of 19M elements each in the time it took the naive algorithm to process just 3.6M elements.

Most interesting to me is the performance of the transpose algorithm. As discussed earlier, the improvements to cache performance, at the expense of a full matrix copy, are clearly demonstrated in those results – even with an algorithm asymptotically equivalent to the naive approach.

Profiling and performance optimization

This documentation was a fantastic resource for understanding Rust performance fundamentals. Getting Instruments up and running for profiling on Mac OS was trivial thanks to the Rust guide for cargo-instruments. This is a great tool for both investigating allocation behavior, CPU hot spots, and other things.

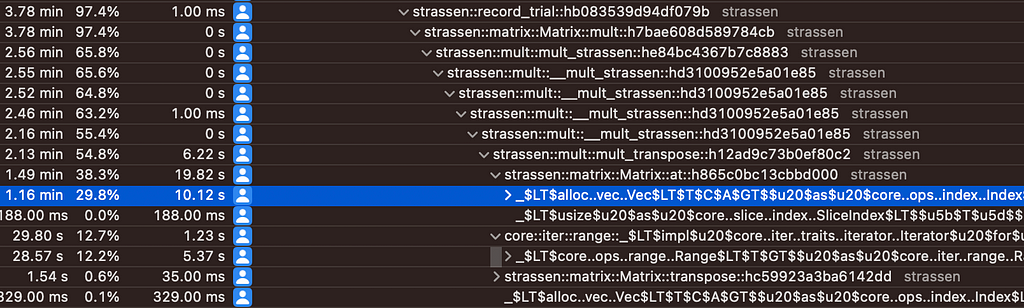
Some changes along the way:

  • The Strassen code calls itself recursively via a divide-and-conquer strategy, but once the matrices reach a small enough size, its high constant factor makes it slower than the general matrix algorithm. I found that this point was a row or column width of about 64; increasing this threshold from 2 improved throughput by several factors
  • The Strassen algorithm calls for a matrix padding up to the nearest exponent of 2; reducing this to lazily ensure matrices had just an even number of rows and columns improved throughput by about double via reduction of expensive large allocations
  • Changing the small-matrix fallback algorithm from naive to transpose led to about a 20% improvement
  • Adding codegen-units = 1 and lto = “thin” to Cargo.toml release build flags was about a 5% improvement. Interestingly lto = “true” made performance consistently worse
  • Meticulously removing all possible Vec copies was about a ~10% improvement
  • Providing a couple#[inline] hints and removing vector bounds checking in random-access lookups resulted in about another 20% improvement
    /**
     * Returns the element at (i, j). Unsafe.
     */
    #[inline]
    pub fn at (&self, i: usize, j: usize) -> f64 {
         unsafe {
            return *self.elements.get_unchecked(i * self.cols + j);
        }
    }

Better-than-Cubic Complexity for Matrix Multiplication in Rust was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.

Previous Post
Next Post