This post started out as a Twitter thread. The text below is the same as that of the thread after correcting an error in the first part of the thread.
***
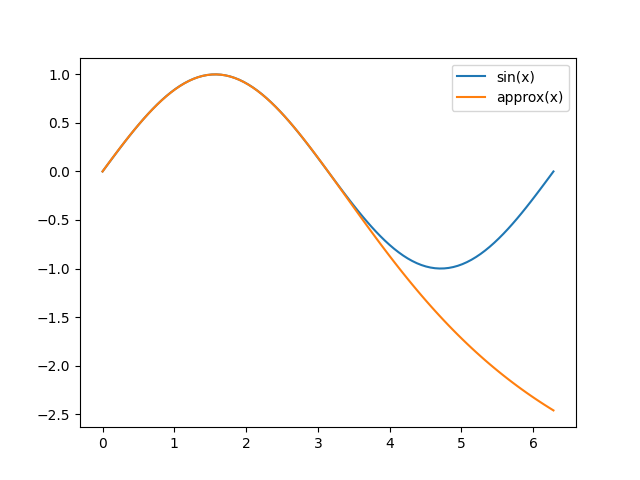
The following approximation for sin(x) is remarkably accurate for 0 < x < π.
The approximation is so good that you can’t see the difference between the exact value and the approximation until you get outside the range of the approximation.
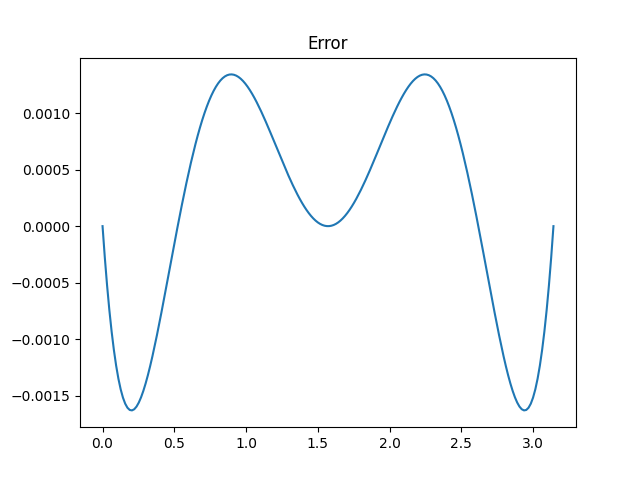
Here’s a plot of just the error.
This is a very old approximation, dating back to Aryabhata I, around 500 AD.
In modern terms, it is a rational approximation, quadratic in the numerator and denominator. It’s not quite optimal since the ripples in the error function are not of equal height, but the coefficients are nice numbers.
The post Ancient accurate approximation for sine first appeared on John D. Cook.