Suppose you take the arithmetic mean and the geometric mean of the first n integers. The ratio of these two means converges to e/2 as n grows [1]. In symbols,
Now suppose we wanted to visualize the convergence by plotting the expression on the left side for a sequence of ns.
First let’s let n run from 1 to 100.
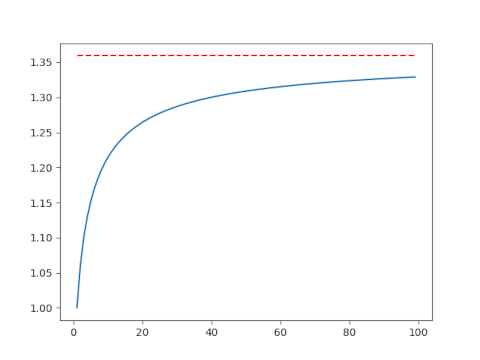
This isn’t very convincing. Maybe the convergence is just slow, or maybe it’s not actually converging to e/2. Let’s make another plot including larger values of n. This will require a little additional work.
Avoiding overflow
Here’s the code that made the plot above.
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import factorial
AM = lambda n: (n+1)/2
GM = lambda n: factorial(n)**(1/n)
n = np.arange(1, 100)
plt.plot(n, AM(n)/GM(n))
plt.plot(n, 0*n + np.exp(1)/2, 'r--')
This works for n up to 170, but it fails when n = 171 because at that point factorial overflows.
This is a very common situation. We ultimately want to compute a fairly small number, but we encounter extremely large numbers in an intermediate step.
We need to avoid directly calculating n! before taking the nth root. The way to do this is to work with logarithms. Now n! = Γ(n+1) and SciPy has a function for computing the log of the gamma function directly without first computing the gamma function, thus avoiding overflow.
We replace GM above with GM2 below:
GM2 = lambda n: np.exp(gammaln(n+1)/n)
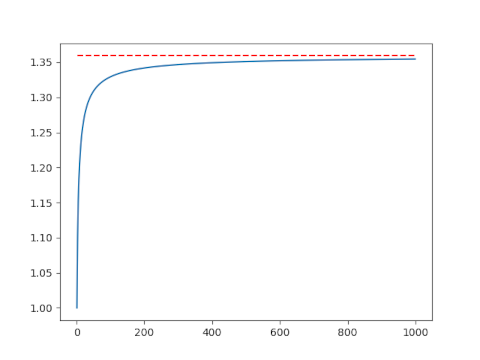
Now we compute the geometric mean of the first n natural numbers for very large values of n. We only need n = 1000 to see convergence, but the code could handle much larger values of n without overflowing.
Related posts
- Arithmetic-harmonic mean
- Avoiding underflow in Bayesian calculations
- Computing soft max without overflow
[1] Richard P. Kubelka. Means to an End. Mathematics Magazine, Vol. 74, No. 2 (April 2001), pp. 141–142
The post AM over GM first appeared on John D. Cook.