Neural network activation functions transform the output of one layer of the neural net into the input for another layer. These functions are nonlinear because the universal approximation theorem, the theorem that basically says a two-layer neural net can approximate any function, requires these functions to be nonlinear.

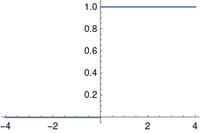
Activation functions often have two-part definitions, defined one way for negative inputs and another way for positive inputs, and so they’re ideal for Iverson notation. For example, the Heaviside function plotted above is defined to be

Kenneth Iverson’s bracket notation, first developed for the APL programming language but adopted more widely, uses brackets around a Boolean expression to indicate the function that is 1 when the expression is true and 0 otherwise. With this notation, the Heaviside function can be written simply as

Iverson notation is fairly common, but not quite so common that I feel like I can use it without explanation. I find it very handy and would like to popularize it. The result of the post will give more examples.

ReLU

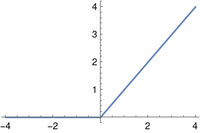
The popular ReLU (rectified linear unit) function is defined as

and with Iverson bracket notation as

The ReLU activation function is the identity function multiplied by the Heaviside function. It’s not the best example of the value of bracket notation since it could be written simply as max(0, x). The next example is better.

ELU

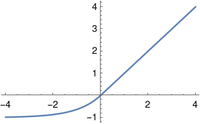
The ELU (exponential linear unit) is a variation on the ReLU that, unlike the ReLU, is differentiable at 0.

The ELU can be described succinctly in bracket notation.

PReLU

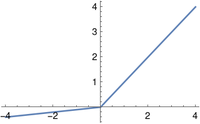
The PReLU (parametric rectified linear unit) depends on a small positive parameter a. This parameter must not equal 1, because then the function would be linear and the universal approximation theorem would not apply.

In Iverson notation:

Related posts

• Smoothed step function
• How to compute softmax
• Floor, ceiling, bracket

The post Activation functions and Iverson brackets first appeared on John D. Cook.