John Conway et al [1] give the name gnu(n) to the number of groups of order n, where “gnu” stands for group number. This function has been studied since the 19th century, but I don’t know whether there has ever been a standard notation for it. Mathematica calls it FiniteGroupCount. It’s also the first sequence in OEIS.

When n is square-free, there is a formula due to Hölder that computes gnu(n). But in general computing gnu(n) is hard. However, [1] gives a surprisingly good heuristic for estimating gnu(n).

Let Ω(n) be the number of prime factors of n, counted with multiplicity. So, for example, Ω(75) = 3 because 3 is a factor with multiplicity 1 and 5 is a factor with multiplicity 2.

Let B(n) be the nth Bell number, the number is the number of ways to partition a set of n labeled items.

The heuristic estimate for gnu(n) is

gnu(n) ≈ B( Ω(n) ).

This can be implemented in Python as follows.

    from sympy import bell, primeomega
    def estimate(n): return bell(primeomega(n))

The following plot shows the exact and approximate values of gnu(n) for n = 1, 2, 3, …, 100.

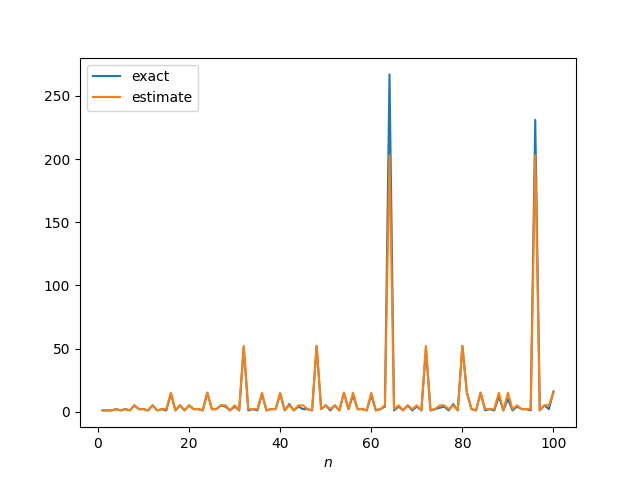
The exact value was plotted first in blue, then the estimate was plotted in orange. The orange line matches the blue so well as to hide it, except at the two spikes where gnu(n) is largest.

Here’s a plot of the errors.

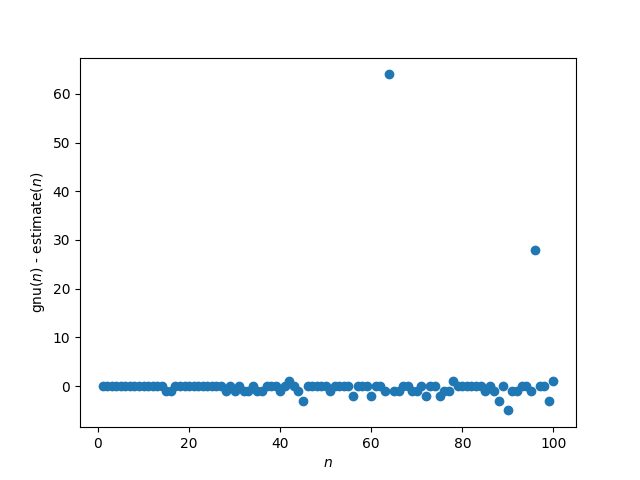
Aside from the two outliers, the error is between −5 and 1.

[1] John H. Conway, Heiko Dietrich and E.A. O’Brien. Counting groups: gnus, moas and other exotica

The post Estimating number of groups of a given order first appeared on John D. Cook.