The relation between a function and its power series is subtle. In a calculus class you’ll see equations of the form “series = function” which may need some footnotes. Maybe the series only represents the function over part of its domain: the function extends further than the power series representation.
Starting with the power series, we can ask whether the function it represents extends further than the series representation.
This video does a nice job of explaining why a particular function cannot be extended beyond the disk on which the series converges.
Toward the end, the video explains how its main example is a member of a broader class of functions that have no analytic continuation. The technical term, which the video does not use, is lacunary series [1]. When the gaps in a power series grow faster than linearly, the series cannot be extended beyond its radius of convergence.
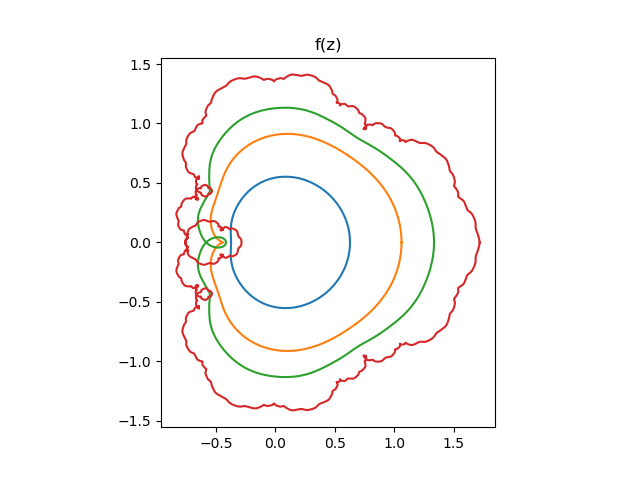
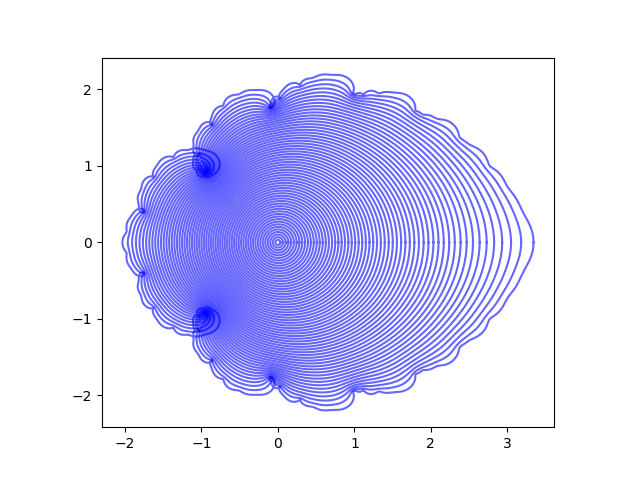
Lacunary series make interesting images since the behavior of the function becomes complicated toward the edge of the domain. The video gives some nice examples. The image above comes from this post and the following image comes from this post.
Differential equations
The video mentions Hadamard’s gap theorem. I believe his gap theorem was a spin-off of his work on Laplace’s equation. See this post on Hadamard’s counterexample to the Dirichlet principle for the Laplacian.
The motivation for a LOT of classical math was differential equations. I didn’t realize this as a student. Years later I’d run into something and think “So that is why this person was interested in that problem,” such as why Hadamard would care about whether power series could be extended.
Hadamard wanted to solve a differential equation on a disk with boundary conditions specified on the rim. It’s going to be a problem if the series representation of the solution doesn’t extend to the rim.
Related posts
[1] Lacuna is the Latin word for a hole or a pit. The word came to be use metaphorically for a gap, such as a gap in a manuscript. Later mathematicians used this term for power series with increasing gaps between non-zero terms.
The post When a function cannot be extended first appeared on John D. Cook.