A function f of a complex variable z = x + iy can be factored into real and imaginary parts:
where x and y are real numbers, and u and v are real-valued functions of two real values.
Suppose you are given u(x, y) and you want to find v(x, y). The function v is called a harmonic conjugate of u.
Finding v
If u and v are the real and imaginary parts of an analytic function, then u and v are related via the Cauchy-Riemann equations. These are first order differential equations that one could solve to find u given v or v given u. The approach I’ll present here comes from [1] and relies on algebra rather than differential equations.
The main result from [1] is
So given an expression for u (or v) we evaluate this expression at z/2 and z/2i to get an expression for f, and from there we can find an expression for v (or u).
This method is simpler in practice than in theory. In practice we’re just plugging (complex) numbers into equations. In theory we’d need to be a little more careful in describing what we’re doing, because u and v are not functions of a complex variable. Strictly speaking the right hand side above applies to the extensions of u and v to the complex plane.
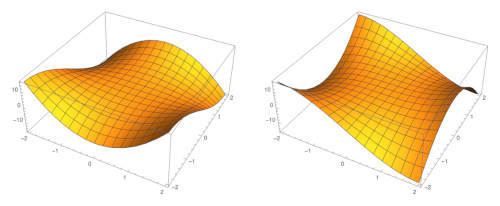
Example 1
Shaw gives three exercises for the reader in [1]. The first is
We find that
We know that the constant term is purely imaginary because u(0, 0) = 0.
Then
and so
is a harmonic conjugate for u for any real number β.
The image above is a plot of the function u on the left and its harmonic conjugate v on the right.
Example 2
Shaw’s second example is
We begin with
and so
From there we find
Example 3
Shaw’s last exercise is
Then
This leads to
from which we read off
Related posts
[1] William T. Shaw. Recovering Holomorphic Functions from Their Real or Imaginary Parts without the Cauchy-Riemann Equations. SIAM Review, Dec., 2004, Vol. 46, No. 4, pp. 717–728.
The post Finding the imaginary part of an analytic function from the real part first appeared on John D. Cook.