
My first hobby project for learning Rust was implementing cryptographic hash algorithms [MD5, SHA-2, SHA-3]. The latter, SHA-3, was the most challenging implementation.
That was due to a) substantial differences in algorithm design from the more familiar MD5 and SHA predecessors and b) fewer and less intuitive reference implementations and algorithm explanations. In this article, I’ll briefly summarize some high-level differences between SHA-3 and earlier algorithms and then walk through its implementation.
The high-level structure of MD5, SHA-1, and SHA-2 is fairly similar; these algorithms are based on the Merkle-Damgård Construction. This is a specific methodology for sequentially chaining chunks of the input message together through a one-way compression function (which may be a composite of several different operations). These are also often built from block ciphers.
From ten thousand feet, these algorithms look like this:
MDHash(M: message):
bytes P = padding (M) // extends length to a multiple of N bits
bytes S = initial working state default values
for chunk in P:
S += compression_function(S, chunk)
return S
The compression function performs a series of nonlinear bitwise mixing of state, constant values, and message input bits. Here’s an example from part of SHA-2’s compression function:
// See https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf # 6.2.2
while indx < 64 {
/*
* From https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf # 4.1.2
*
* The functions Σ0, Σ1, Ch(x, y, z) and Maj(x, y, z)
*/
let s0 = state.a.rotate_right(2) ^ state.a.rotate_right(13)
^ state.a.rotate_right(22);
let s1 = state.e.rotate_right(6) ^ state.e.rotate_right(11)
^ state.e.rotate_right(25);
let ch = (state.e & state.f) ^ ((!state.e) & state.g);
let maj = (state.a & state.b) ^ (state.a & state.c) ^ (state.b & state.c);
// See https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf
// # 6.2.2 section 3
state.rotate(
state.h.wrapping_add(s1)
.wrapping_add(ch)
.wrapping_add(K[indx])
.wrapping_add(w[indx]),
s0.wrapping_add(maj)
);
indx += 1;
}
This hash construction technique suffers from a variety of vulnerabilities, and the approach taken in SHA-3 is different.
SHA-3 was released by NIST in 2015 and is based on a hash algorithm called Keccak, introduced in 2012. I’ll use these terms interchangeably below. Rather than relying on the Merkle-Damgård process, SHA-3 / Keccak uses a technique called sponge construction.
From ten thousand feet, it looks roughly like this:
SHA-3(M: message, N: digest length):
bytes P = padding (M) // extends length to a multiple of N bits
bytes S = 0x0 // state
// "absorb"
for chunk in P:
S[index] ^= chunk
permute(S) // mix entire state
bytes output = []
// "squeeze"
while output length < N:
output += S[0...M]
permute(S) // mix entire state
return output
I won’t try to cover many complex properties of this approach here. A couple of high-level points are:
- The length of the state array in bits is not 1:1 with the intended digest output size or content. Instead, prefix chunks are iteratively pulled out of the state
- During digest computation, the state is further permuted upon reaching the end of each state chunk. This process repeats until the output buffer has reached its intended length.
I’ll walk through how SHA-3 works in more detail below.
Padding
Padding is straightforward in SHA-3 and resembles approaches to padding in earlier hash algorithms. The goal of padding is to extend the length of the input message to a multiple of the “rate,” a value defined in this table as r , allowing for easy chunking.
A 0x06 must be appended right after the message, even if the message is already a multiple of r. Zero or more zero bytes are added until the array length is 1 byte less than a multiple of r, and then a 0x80 is concatenated as the last byte.
In the special case where the input message length is equal to r — 1, these two delimiters are concatenated together as 0x06 | 0x80 in a single byte.
You can see this implementation here in Rust.
fn pad (message: &mut Vec<u8>, rate: usize) {
let rate_bytes = rate / 8;
if message.len() == rate_bytes - 1 {
// Special case. 0x06 and 0x80 must always be present.
// If the message length is 1 byte less than a
// multiple of the rate, append these two values OR'd together
// so the last byte is 0x86
message.push(0x06 | 0x80);
} else {
// Messages are padded to something like
// [... 0x06, 0x0, 0x0 ..., 0x80]
message.push(0x06);
while (message.len() % rate_bytes) != rate_bytes - 1 {
message.push(0x0);
}
message.push(0x80);
}
}
One interesting note, however, is that the SHA-3 specification introduces a slight change from the Keccak algorithm specification — in the padding definition. The Keccak algorithm appends 0x01 right after the message:
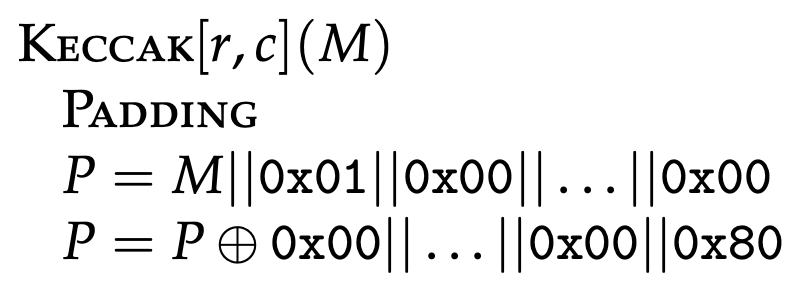
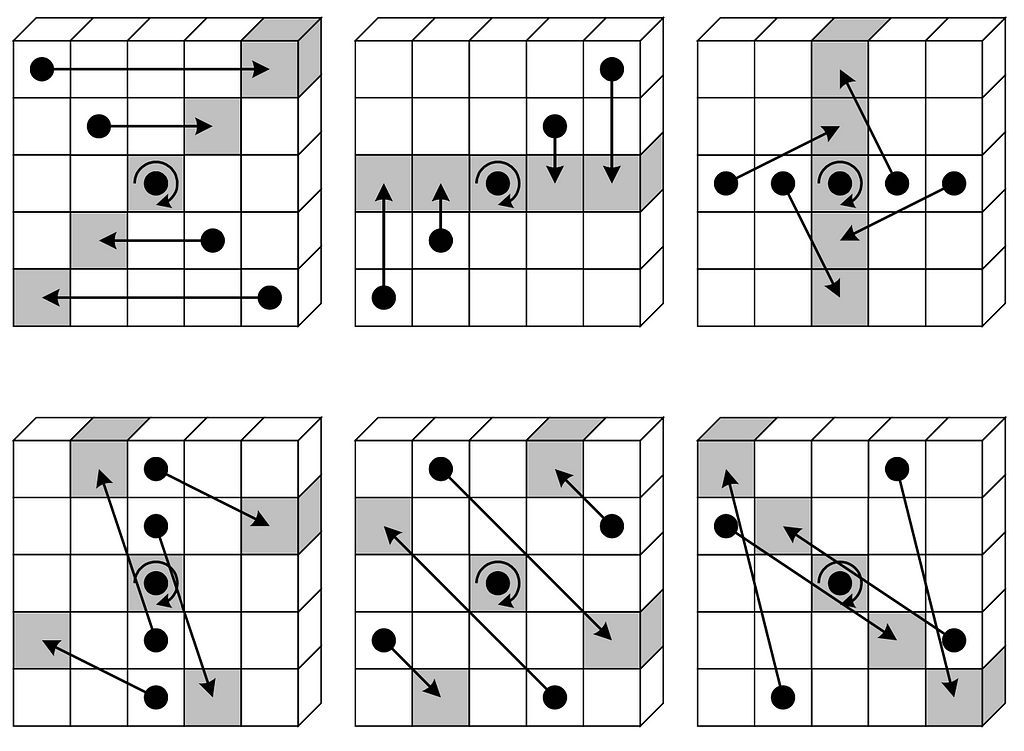
The SHA-3 specification changed the initial 0x1 to 0x6. This means that even though SHA-3 is based on Keccak, the Keccak hash of a message will result in a different digest output than SHA-3. The difference here is just three bits in the padding, but the digest value will be completely different due to the avalanche effect.
State, Chunking, and Absorbing
The algorithm specification defines the state array as a three-dimensional array of bits, depending on the configuration and value of parameter w, ranging from 25 to 1600 total bits.
This state modeling wasn’t particularly helpful for me; it was much easier to think about the state as a 5×5 array of 64-bit integers (u64), which captured the maximal state size of 1600 bits. Unlike other hash algorithms, the state isn’t initialized to a set of magic numbers but just to zero.
The input message is chunked into 512-bit blocks, which is equivalent to 8 u64. Each of these integers is then “absorbed” into the state, which means XOR-ing the inbound integer into a corresponding location in the state.
// Each 512-bit chunk is further broken into 8 64-bit words;
// each is independently absorbed into the state array
for chunk in block.chunks(8) {
// Convert message byte chunks into a little-endian u64 integer
let (b1, b2, b3, b4, b5, b6, b7, b8)
= (chunk[0] as u64, chunk[1] as u64, chunk[2] as u64, chunk[3] as u64,
chunk[4] as u64, chunk[5] as u64, chunk[6] as u64, chunk[7] as u64);
let word = (b8 << 56) | (b7 << 48) | (b6 << 40) | (b5 << 32)
| (b4 << 24) | (b3 << 16) | (b2 << 8) | b1;
state.absorb(indx, word);
indx += 1;
}
fn absorb (&mut self, indx: usize, word: u64) {
// Some transformation from single index to element in this 2D state array
self.state[indx / 5][indx % 5] ^= word;
}
After each block of eight u64 chunks is absorbed, the state is permuted.
Permutation
The permutation step is 24 rounds of execution of five functions on the state data. Each round results in an irreversible intermediate permutation of bits in the state.
/**
* From https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf # 3.3
*
* Given a state array A and a round index ir, the round function Rnd
* is the transformation that results from applying the
* step mappings θ, ρ, π, χ, and ι, in that order, i.e.:
* Rnd(A, ir) = ι(χ(π(ρ(θ(A)))), ir).
*
* See also https://keccak.team/keccak_specs_summary.html for pseudo-code
* descriptions of this permutation, its 24 rounds, and
* the underlying functions.
*/
fn permute (&mut self) {
for i in 0..24 {
self.theta();
self.rho_and_pi();
self.chi();
self.iota(i);
}
}
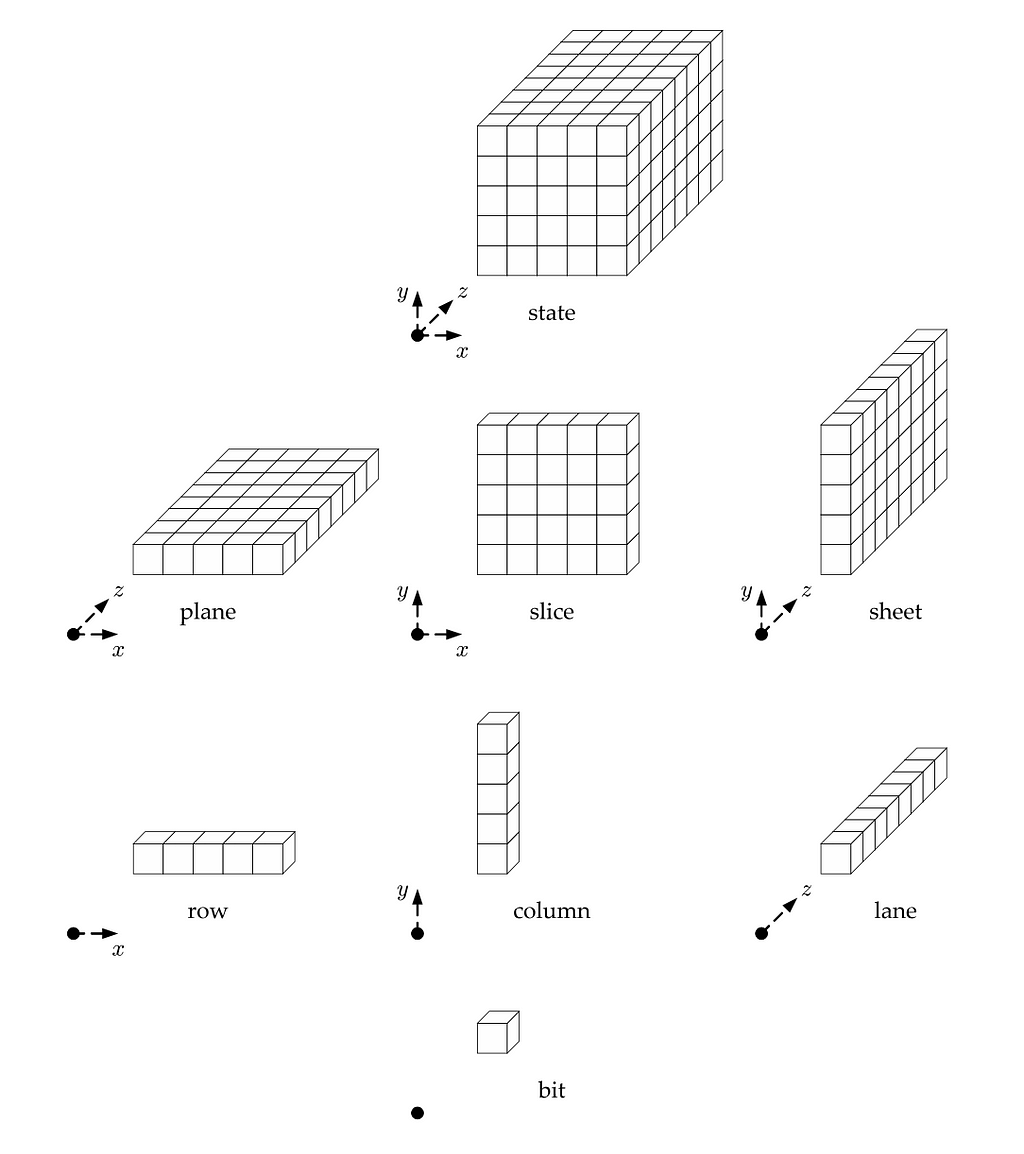
Each of these functions performs a mutation on some plane of the state array. For example, the effect of rho is illustrated here, visualizing a “sheet” or column of full integers in the state, using the 3D state modeling from earlier:
This particular function performs an integer rotation on each u64 in the state array, where the rotation offsets are defined in the Keccak summary. This particular function is coupled with pi, which rotates the placement of each u64 in the state array. It’s a little like rotating a Rubik’s Cube.
I’ve taken care to describe and cite the specific implementation details of each of these functions (theta, rho, pi, chi, iota) in code for those interested.
Squeezing
The final step is extracting the contents of the state array into an output byte vector before base-64 encoding. I found the Keccak pseudocode unintuitive; the NIST pseudocode under “sponge construction” was clearer.

In Rust
/**
* From https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf
* # 4 and Algorithm 8, steps 7 to 10
*
* This function extracts bytes from the state array and returns
* a vector capturing the number of digest bytes corresponding to
* the request digest output size.
*/
fn squeeze (&mut self, rate: usize, md_size: usize) -> Vec<u8> {
let num_words = rate / 64;
let len_bytes = md_size / 8;
let mut bytes = Vec::with_capacity(len_bytes * 2);
// Iterates until sufficient bytes have been read to fill the
// final message digest byte vector
while bytes.len() < len_bytes {
// Read the first 'num_words` integers from the state array
for i in 0..num_words {
bytes.extend_from_slice(&self.state[i / 5][i % 5].to_le_bytes());
}
if bytes.len() < len_bytes {
// If we have more bytes to read, permute
// the state for the next round of reading
self.permute();
}
}
// Return the first len_bytes of the result, consistent
// with requested message digest size
return bytes[0..len_bytes].to_vec();
}
Earlier on, I outlined the general differences between this approach and older hash function techniques for extracting digest values from the hash state. The output bytes are pulled in batches from the beginning of the state array (as in state[0][0]). After reaching a certain length, the rest of the state is discarded, and the entire array goes through another round of 24 permutations.
The final step is encoding the bytes in base 64.
~/code/sha-3 ~>> ./target/release/sha3 --algo 224 --string rust
c44aa66c6a741d515297a91554d6a669323288ba1d42a7402938e5df
~/code/sha-3 ~>> ./target/release/sha3 --algo 256 --string rust
dcd84e60f950eebbeaf1db530fd4ed1ccf61aab94b558653072a205fb0fedee7
~/code/sha-3 ~>> ./target/release/sha3 --algo 384 --string rust
e7e13b16b131f1a8bc3ef00601beb13031d82de118bf5204757d3f5d8fa3c69431d0944ed9ee8cfd479acb0b16a93941
~/code/sha-3 ~>> ./target/release/sha3 --algo 512 --string rust
31805399bdec85ad94582da495b92cc3054835ac97d475ff1946ba85b2d9bd02f6ac2d8ccc6b72622de5c63a5eee28c1323bfec26fc56116193ae988c59b3bc8
~/code/sha-3 ~>> time ./target/release/sha3 --test
[OK] SHA3-224 ("")
[OK] SHA3-224 ("abcde")
[OK] SHA3-224 ("6acfaab70afd8439cea3616b41088bd81c939b272548f6409cf30e57")
[OK] SHA3-256 ("")
[OK] SHA3-256 ("abcde")
[OK] SHA3-256 ("d716ec61e18904a8f58679b71cb065d4d5db72e0e0c3f155a4feff7add0e58eb")
[OK] SHA3-384 ("")
[OK] SHA3-384 ("abcde")
[OK] SHA3-384 ("348494236b82edda7602c78ba67fc3838e427c63c23e2c9d9aa5ea6354218a3c2ca564679acabf3ac6bf5378047691c4")
[OK] SHA3-512 ("")
[OK] SHA3-512 ("abcde")
[OK] SHA3-512 ("1d7c3aa6ee17da5f4aeb78be968aa38476dbee54842e1ae2856f4c9a5cd04d45dc75c2902182b07c130ed582d476995b502b8777ccf69f60574471600386639b")
All 12 tests completed successfully!
real 0m0.007s
user 0m0.002s
sys 0m0.003s
For readers looking for a plain walkthrough or readable implementation of SHA-3, hopefully, you found this useful.
Rust
As for Rust itself, here are a few thoughts:
- As someone used to C and C++, I found fighting with the Rust type and safety systems frustrating — at first
- Once the programs compiled, it was nice to run them without having to debug segmentation faults then
- I thought many of the built-in collection and primitive type methods were handy, intuitive, and very well documented
- Performance of these programs seems comparable to built-in MacOS native hash utilities
- Cargo is just fantastic for package and dependency management
Learning Rust With SHA-3 and Friends was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.