Let A, B, C, and D be positive numbers. Then Lehman’s inequality says
Proof by circuit
This inequality can be proved analytically, but Lehman’s proof is interesting because he uses electrical circuits [1].
Let A, B, C, and D be the resistances of resistors arranges as in the circuit on the left.
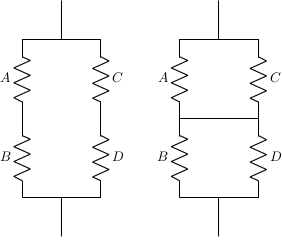
Resistors R1 and R2 in series have a combined resistance of
and the same resistors in parallel have a combined resistance of
This means the circuit on the left has combined resistance
The resistance of the circuit on the right is
Adding a short cannot increase resistance, so the resistance of the circuit on the right must be the same or lower than the resistance of the one on the left. Therefore
Drawing circuits in LaTeX
I drew the circuits above using the circuitikz package in LaTeX. Here’s the code to draw the circuit on the left.
documentclass{article}
usepackage{tikz}
usepackage{circuitikz}
begin{document}
begin{figure}[h!]
begin{center}
begin{circuitikz}
draw (0,0)
to[R=$B$] (0,2)
to[R=$A$] (0,4)
to[short] (2,4)
to[R=$C$] (2,2)
to[R=$D$] (2,0)
to[short] (0,0);
draw (1,4)
to[short] (1, 5);
draw (1, 0)
to[short] (1, -1);
%draw (0, 2)
%to[short] (2, 2);
end{circuitikz}
end{center}
end{figure}
end{document}
The code to draw the second circuit removes the %’s commenting out the code that draws the short between the two parallel arms of the circuit.
[1] Alfred Lehman proves a more general result using circuits in SIAM Review, Vol. 4, No. 2 (April 1962) pp. 150–151. Fazlollah Reza gives a purely mathematical proof on pages 151 and 152 of the same journal.
The post Lehman’s inequality, circuits, and LaTeX first appeared on John D. Cook.