A comprehensive, easy-to-follow exploration of Torchquad’s revolutionary GPU-accelerated numerical integration. Integrate 10x faster than any other library in Python

In the realm of modern science and engineering, integration plays a pivotal role. It is the foundation of many calculations, from solving complex differential equations to computing areas under curves. However, as computations become more complex and data-intensive, traditional methods often fall short, consuming significant time and resources. Enter Torchquad, a cutting-edge Python package set to change the game.

Short Intro to Numerical Integration
Numerical integration is a fundamental method used in mathematics and computational science to approximate definite integrals. It is a technique employed when an analytical solution to an integral is difficult to obtain or when the function to be integrated available only as data points. While analytical integration provides exact solutions, numerical integration provides approximate solutions, which is more than adequate for many real-world problems.
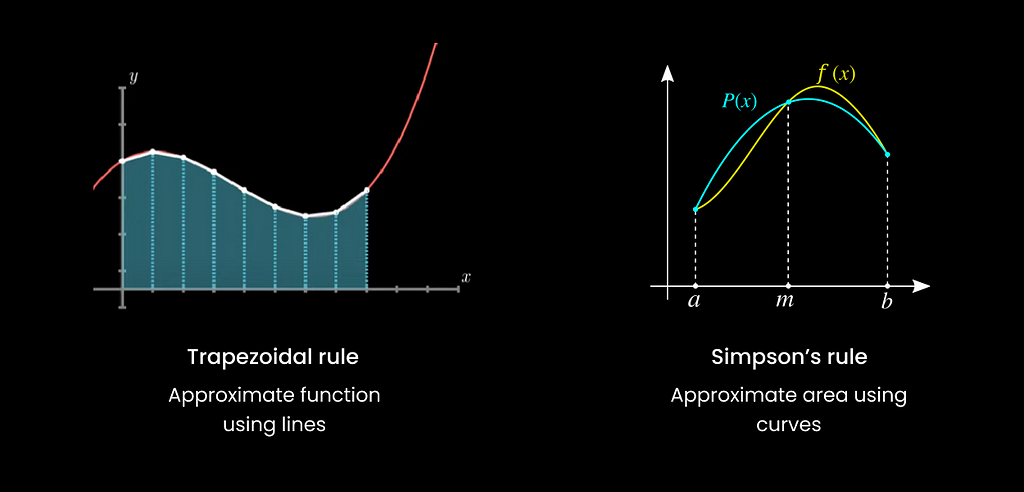
There are various methods of numerical integration:
- Trapezoidal rule
- Simpson’s rule
- Gaussian quadrature
- Monte-Carlo method
Each method has its own strengths and weaknesses depending on the nature of the function being integrated and the precision required. The trapezoidal rule, for example, uses a series of trapezoids to estimate the area under a curve, whereas Simpson’s rule uses parabolas. The Gaussian quadrature, on the other hand, is a more advanced method that provides high precision for polynomial functions.
While these traditional numerical integration methods have proven useful, they can become computationally expensive when dealing with high-dimensional integrals or large datasets. Each additional data point significantly increases the computation time in such scenarios, making these methods less feasible. This is where new methods and computational tools, such as Torchquad, come into play, leveraging the power of GPU acceleration to perform numerical integration at much faster speeds and with greater accuracy.
Installation Guide
First, you must be sure that you have installed PyTorch with CUDA support. For this, you can follow this tutorial.
When you have PyTorch with CUDA support installed, you can run these lines in your console:
Conda
conda install torchquad -c conda-forge
Python
pip install torchquad
After installing Torchquad, you can test that everything works by running this code in a Jupyter Notebook/Python script:
import torchquad
torchquad._deployment_test()
If you encounter issues, you can visit the official documentation:
- GitHub – esa/torchquad: Numerical integration in arbitrary dimensions on the GPU using PyTorch / TF / JAX
- PyTorch
Examples
First of all, import all the necessary libraries:
import numpy as np
import torch
import sympy as smp
import matplotlib.pyplot as plt
from torchquad import Simpson, MonteCarlo, set_up_backend
from scipy.integrate import quad
Then, we need to set up our backend and GPU support:
# Enable GPU support if available and set the floating point precision
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device) # This will print "cuda" if everything work correctly
set_up_backend("torch", data_type="float32")
Now, our first problem. Suppose that we need to solve this integral numerically:

With scipy, it would look like this:
def integrand(x):
return np.cos(x) / (1 + np.sin(x))
quad(integrand, 0, np.pi/2)
# (0.6931471805599454, 7.695479593116622e-15)
In Torchquad, we have to use PyTorch functions, so it will look like this:
def integrand_pytorch(x):
return torch.cos(x) / (1 + torch.sin(x))
integrator = Simpson() # Initialize Simpson solver
integrator.integrate(integrand_pytorch, dim=1, N=999999,
integration_domain=[[0, np.pi/2]],
backend="torch",)
# 0.6931
We can use different integrators, for example, the Monte-Carlo method:
def integrand_pytorch(x):
return torch.cos(x) / (1 + torch.sin(x))
integrator = MonteCarlo() # Initialize Simpson solver
integrator.integrate(integrand_pytorch, dim=1, N=999999,
integration_domain=[[0, np.pi/2]],
backend="torch",)
# 0.6927
You can see that the error is now bigger, as the true value is closer to 0.6931, but this time we have 0.6927.
Now, our second problem — 5D integral:

Here’s what that looks like in Scipy:
%%timeit
def integrand(*x):
return np.sum(np.sin(x))
nquad(integrand, [[0, 1]] * 5)[0]
# Result: 2.2984884706593016
# Time: 31.8 s ± 594 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Torchquad:
def integrand_pytorch(x):
return torch.sum(torch.sin(x), dim=1)
N = 1000000
integrator = Simpson() # Initialize Simpson solver
integrator.integrate(integrand_pytorch, dim=5, N=N, integration_domain=[[0, 1]] * 5)
# Result: 2.2985
# Time: 3.59 ms ± 113 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
You can increase accuracy by using different data types, accuracy (parameter N), and different integrators. You can find all the available integrators here.
Performance
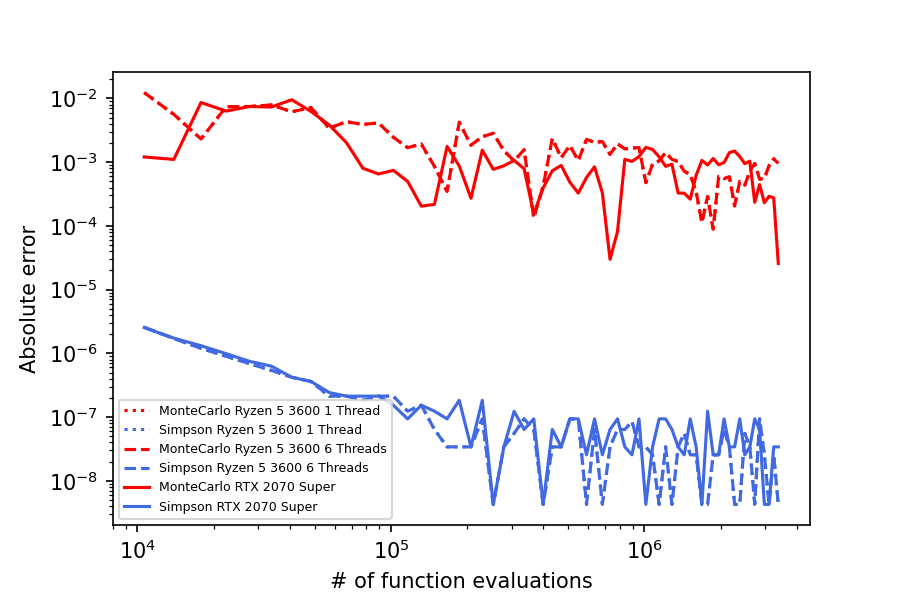
Using GPUs, Torchquad scales particularly well with integration methods that offer easy parallelization. For example, below, you see error and runtime results for integrating the function f(x,y,z) = sin(x * (y+1)²) * (z+1) on a consumer-grade desktop PC.

Conclusion
Numerical integration is essential in the mathematical and computational sciences, often providing the only feasible approach to solving complex, real-world problems. However, as we delve into more intricate computations and larger datasets, traditional methods can fall short, demanding a more powerful solution.
That’s where TorchQuad steps in, revolutionizing the field with its GPU-accelerated approach to numerical integration. By harnessing the speed and efficiency of modern GPUs, it offers a faster, more accurate solution, and is accessible to a wide range of users, from students to seasoned researchers.
References
Want to Connect?
Let's connect on LinkedIn
Follow me on Medium
Torchquad: Python Library for Numerical Integration With GPU Acceleration was originally published in Better Programming on Medium, where people are continuing the conversation by highlighting and responding to this story.