If three circles are all tangent to each other, you can find two more circles that are tangent to all three, and the equation for finding these new circles is remarkably elegant. This is Descartes’ theorem.

Two tangent circles

To illustrate Descartes’ theorem, we first need three mutually tangent circles. Drawing two mutually tangent circles is easy. We choose our coordinate system so that the first circle is centered at the origin

O₁ = (x₁, y₁) = (0, 0)

and the center of the second circle is on the x-axis. If the two circles have radii r₁ and r₂, then the center of the second circle is at

O₂ = (x₂, y₂) = (r₁ + r₂, 0).

I’ve assumed that the second circle is outside the first. You could have a tangent circle inside another circle, but to illustrate Descartes’ theorem we need circles that are externally tangent.

Three tangent circles

Now we pick the radius of the third circle to be r₃. The center of this circle must belong to a circle of radius r₁ + r₃ centered at O₁ and to a circle of radius r₂ + r₃ centered at O₂. I went over finding the point(s) of intersection of two circles here.

For illustration I chose r₁ = 2, r₂ = 1, and r₃ = 2.8. Using the code from the aforementioned post I found

(x₃, y₃) = (2.93333333 3.79941516)

Here’s a plot.

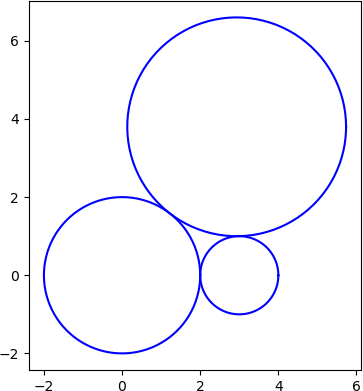
Four tangent circles

Now we’re in a position to state and illustrate Descartes’ theorem. The theorem is most easily stated in terms of signed curvatures.

The curvature of a circle of radius r is 1/r. Big circles have small curvature and small circles have big curvature.

For Descartes’ theorem we need to use signed curvatures, taking the sign to be positive if circles are externally tangent and negative if the circles are internally tangent. The signed curvatures of our three circles are positive, that is

k_i = 1/r_i

for i = 1, 2, and 3. But Descartes’ theorem will give us two circles, one between the three given circles and one surrounding them, corresponding to a positive and negative solution for k₄.

Finding the radii

Now we can state Descartes’ theorem [1]:

(k₁ + k₂ + k₃ + k₄)² = 2(k₁² + k₂² + k₃² + k₄²)

This gives us a quadratic equation for k₄ with two solutions:

k₄ = k₁ + k₂ + k₃ ±2(k₁k₂ + k₂k₃ + k₁k₃)^½.

Finding the centers

Now we know the radii of our tangent circles, but not the centers. For this we view the circles as living in the complex plane with centers z_i. Then the centers satisfy a theorem analogous to the one satisfied by the curvatures.

(k₁z₁ + k₂z₂ + k₃z₃ + k₄z₄)² = 2(k₁²z₁² + k₂²z₂² + k₃²z₃² + k₄²z₄²)

I’m unclear on the history here, but I don’t believe Descartes had a formula for the centers of the circles. He certainly did not have the formula above using complex numbers [2].

Here’s a plot of the two circles guaranteed by Descartes’ theorem.

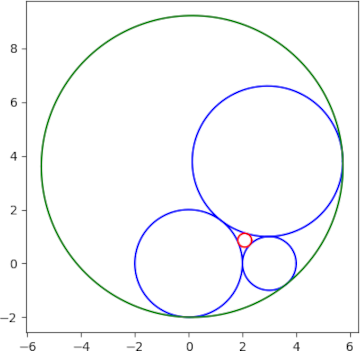
[1] The Soddy-Gossett theorem generalizes Descartes theorem to the case of n + 2 spheres in ℝⁿ. The square of the sums of the curvatures equals n the sum of the curvatures squared.

[2] Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks. Beyond the Descartes circle theorem. https://arxiv.org/abs/math/0101066v1

The post Finding tangent circles first appeared on John D. Cook.