Casting out nines is a well-known way of finding the remainder when a number is divided by 9. You add all the digits of a number n. And if that number is bigger than 9, add all the digits of that number. You keep this up until you get a number less than 9.

This is an example of persistence. The persistence of a number, relative to some operation, is the number of times you have to apply that operation before you reach a fixed point, a point where applying the operation further makes no change.

The additive persistence of a number is the number of times you have to take the digit sum before getting a fixed point (i.e. a number less than 9). For example, the additive persistence of 8675309 is 3 because the digits in 8675309 sum to 38, the digits in 38 sum to 11, and the digits in 11 sum to 2.

The additive persistence of a number in base b is bounded above by its iterated logarithm in base b.

The smallest number with additive persistence n is sequence A006050 in OEIS.

Multiplicative persistence is analogous, except you multiply digits together. Curiously, it seems that multiplicative persistence is bounded. This is true for numbers with less than 30,000 digits, and it is conjectured to be true for all integers.

The smallest number with multiplicative persistence n is sequence A003001 in OEIS.

Here’s Python code to compute multiplicative persistence.

def digit_prod(n):
    s = str(n)
    prod = 1
    for d in s:
        prod *= int(d)
    return prod

def persistence(n):
    c = 0
    while n > 9:
        n = digit_prod(n)
        print(n)
        c += 1
    return c   

You could use this to verify that 277777788888899 has persistence 11. It is conjectured that no number has larger persistence larger than 11.

The persistence of a large number is very likely 1. If you pick a number with 1000 digits at random, for example, it’s very likely that at least of these digits will be 0. So it would seem that the probability of a large number having persistence larger than 11 would be incredibly small, but I would not have expected it to be zero.

Here are plots to visualize the fixed points of the numbers less than N for increasing values of N.

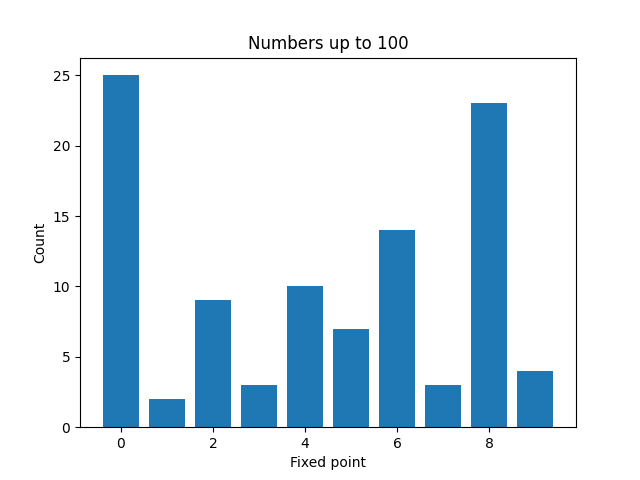
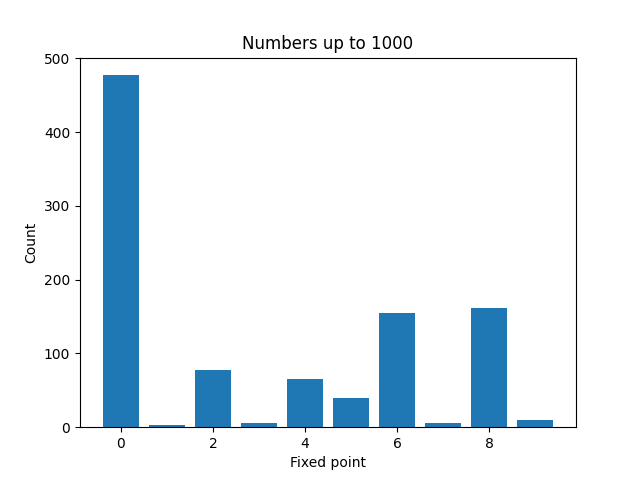
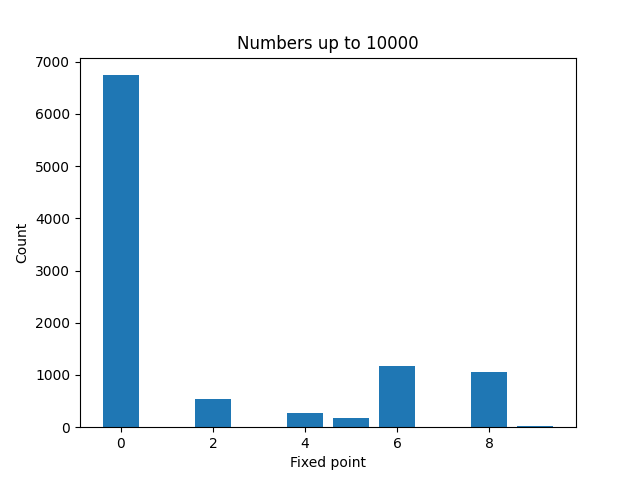
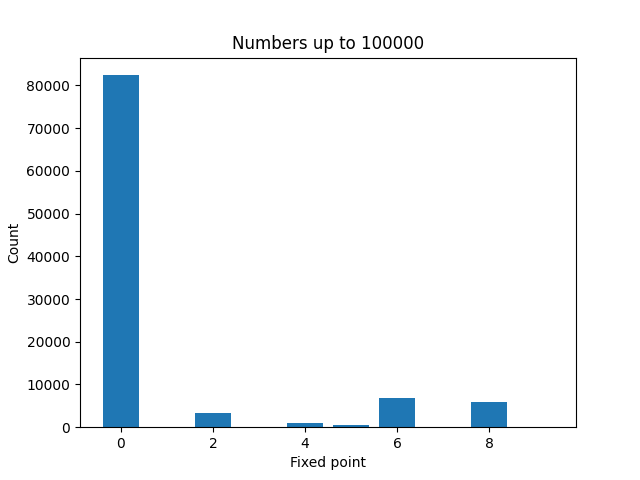
It’s not surprising that zeros become more common as N increases. And a moments thought will explain why even numbers are more common than odd numbers. But it’s a little surprising that 4 is much less common than 2, 6, or 8.

Incidentally, we have worked in base 10 so far. In base 2, the maximum persistence is 1: when you multiply a bunch of 0s and 1s together, you either get 0 or 1. It is conjectured that the maximum persistence in base 3 is 3.

The post Additive and multiplicative persistence first appeared on John D. Cook.