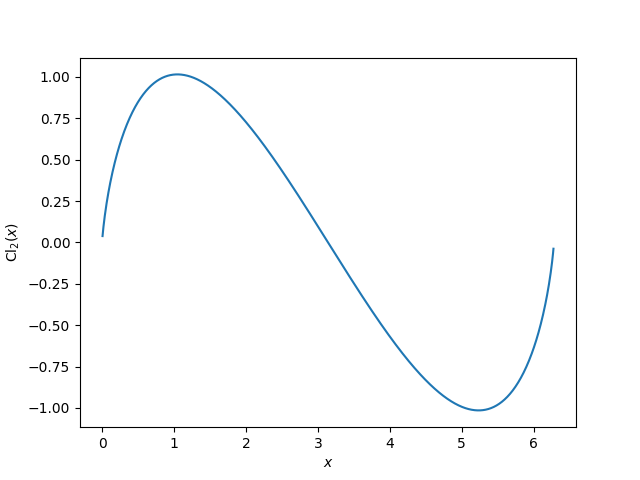
I ran across the Clausen function the other day, and when I saw a plot of the function my first thought was that it looks sorta like a sawtooth wave.
I wondered whether it also sounds like a sawtooth wave, and indeed it does. More on that shortly.
The Clausen function can be defined in terms of its Fourier series:
The function commonly known as the Clausen function is one of a family of functions, hence the subscript 2. The Clausen functions for all non-negative integers n are defined by replacing 2 with n on both sides of the defining equation.
The Fourier coefficients decay quadratically, as do those of a triangle wave or sawtooth wave, as discussed here. This implies the function Cl2(x) cannot have a continuous derivative. In fact, the derivative of Cl2(x) is infinite at 0. This follows quickly from the integral representation of the function.
The fundamental theorem of calculus shows that the derivative
blows up at 0.
Now suppose we create an audio clip of Cl2(440x). This creates a sound with pitch A 440, but rather than a sinewave it has an unpleasant buzzing sound, much like a sawtooth wave.
The harshness of the sound is due to the slow decay of the Fourier coefficients; the Fourier coefficients of more pleasant musical sounds decay much faster than quadratically.
Related posts
The post The Clausen function first appeared on John D. Cook.