In 1609, Kepler remarked that the perimeter of an ellipse with semiaxes a and b could be approximated either as
P1 ≈ 2π(ab)½
or
P2 ≈ π(a + b).
In other words, you can approximate the perimeter of an ellipse by the circumference of a circle of radius r where r is either the geometric mean or arithmetic mean of the semi-major and semi-minor axes.
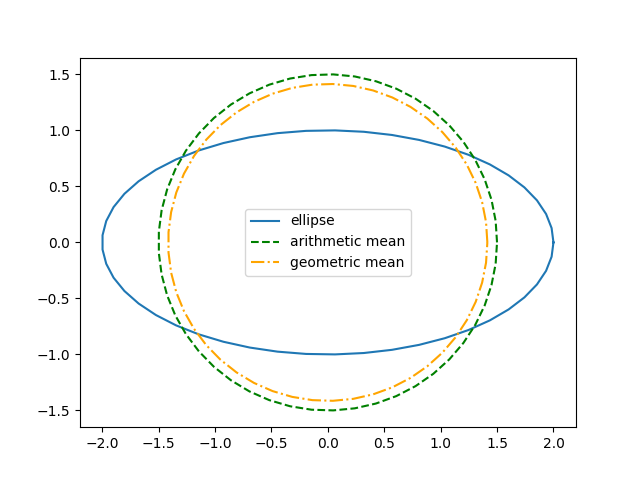
How good are these approximations, particularly when a and b are roughly equal? Which one is better?
When can choose our unit of measurement so that the semi-minor axis b equals 1, then plot the error in the two approximations as a increases.

We see from this plot that both approximations give lower bounds, and that arithmetic mean is more accurate than geometric mean.
Incidentally, if we used the geometric mean of the semi-axes as the radius of a circle when approximating the area then the results would be exactly correct. But for perimeter, the arithmetic mean is better.

Next, if we just consider ellipses in which the semi-major axis is no more than twice as long as the semi-minor axis, the arithmetic approximation is within 2% of the exact value and the harmonic approximation is within 8%. Both approximations are very good when a ≈ b.
More ellipse posts
- Eccentricity, flattening, and aspect ratio
- Conformal map of rectangle to ellipse
- Ellipses and elliptic integrals
The post Kepler’s ellipse perimeter approximations first appeared on John D. Cook.